

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811 ...
In mathematics, the Fibonacci numbers form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors omit the initial terms and start the sequence from 1 and 1 or from 1 and 2. Starting from 0 and 1, the next few values in the sequence are
Reality is a simulation created by algorithms that follow the Fibonacci Sequence - patterns that repeat in the cycles called time.
The brain is a computer that functions on binary code - ones and zeros. Together they form the illusion of what we believe is our reality but in truth it is just a Human Experiment to capture and understand the nature of emotions.

Why does nature love spirals? The link to entropy - a quantity deeply bound to the fabric of space and time. PhysOrg - March 15, 2025
There are moments in the history of human thought when a simple realization transforms our understanding of reality. A moment when chaos reveals itself as structure, when disorder folds into meaning, and when what seemed like an arbitrary universe unveils itself as a system governed by hidden symmetries. The Bekenstein bound was one such revelation - an idea that whispered to us that entropy, information and gravity are not separate but rather deeply intertwined aspects of the cosmos.
In mathematics, the Fibonacci numbers form a sequence defined by the following recurrence relation. The Fibonacci numbers first appeared, under the name matrameru (mountain of cadence), in the work of the Sanskrit grammarian Pingala (Chandah-shastra, the Art of Prosody, 450 or 200 BC). The Fibonacci sequence is named after Italian mathematician Leonardo of Pisa, known as Fibonacci. His 1202 book Liber Abaci introduced the sequence to Western European mathematics. Fibonacci Numbers
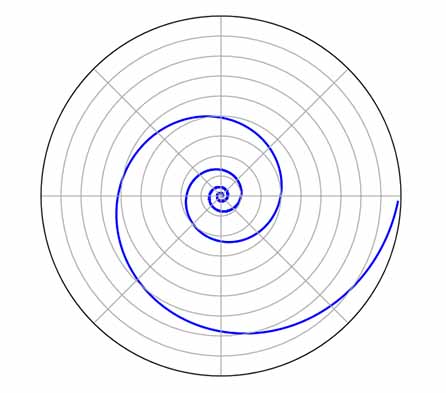
Logarithmic Spiral
The logarithmic spiral, equiangular spiral or growth spiral is a self-similar spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous spiral". Although this curve had already been named by other mathematicians, the specific name ("miraculous" or "marvelous" spiral) was given to this curve by Jacob Bernoulli, because he was fascinated by one of its unique mathematical properties: the size of the spiral increases but its shape is unaltered with each successive curve, a property known as self-similarity. Possibly as a result of this unique property, the spira mirabilis has evolved in nature, appearing in certain growing forms such as nautilus shells and sunflower heads. Jacob Bernoulli wanted such a spiral engraved on his headstone along with the phrase "Eadem mutata resurgo" ("Although changed, I shall arise the same."), but, by error, an Archimedean spiral was placed there instead.

Long-Standing Problem of 'Golden Ratio' and
Other Irrational Numbers Solved with 'Magical Simplicity'
Live Science - September 17, 2019

Golden Ratio, Golden Mean, Golden Section, Divine Proportion

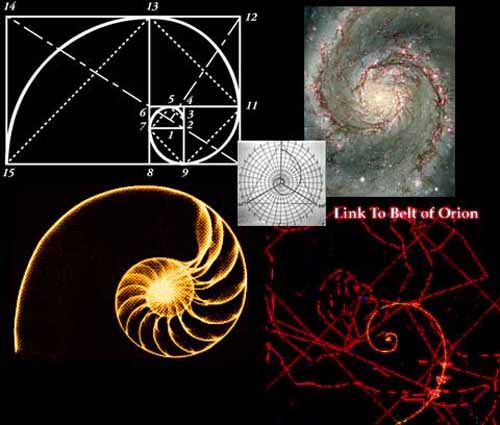
The golden ratio is also called the golden section or golden mean. Other names include extreme and mean ratio, medial section, divine proportion, divine section golden proportion, golden cut, and golden number. Many artists and architects have proportioned their works to approximate the golden ratio - especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio - believing this proportion to be aesthetically pleasing.
Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which can be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data. Read more ...

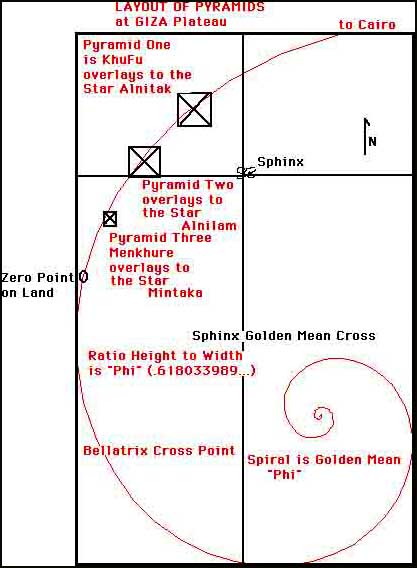
Ancient Pueblo Used Golden Ratio to Build the Sun Temple
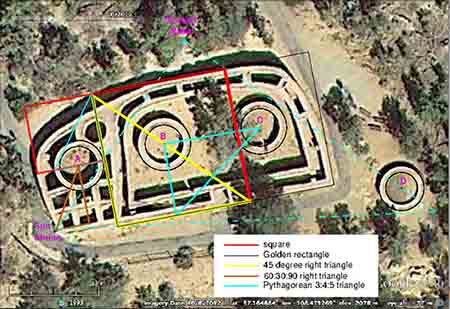
Live Science - February 13, 2017
The Great Pyramids in Giza, the Parthenon in Athens and Chichen Itza in Mexico have something in common. Besides attracting hordes of tourists, all of these architectural wonders appear to use the golden ratio. This mathematical number is often written as 1.618, the first few digits of its infinite decimal form. Expressed another way, two quantities - let's call the larger one "a" and the smaller "b" - are in the golden ratio if "a is to b" as "a + b is to a." The result is a composition with aesthetically pleasing proportions. Now, shapes with the golden ratio, as well as other geometric shapes, have been found in another, unexpected site: the Sun Temple at Mesa Verde National Park in Colorado, built by the ancient Pueblo people who lived in what is now the modern-day Southwest; they had no known written language or written number system.
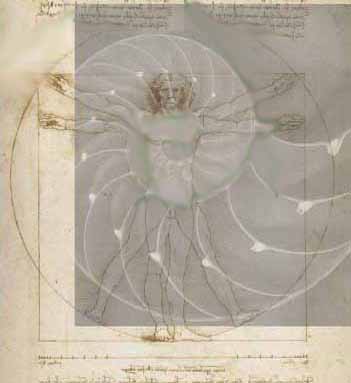
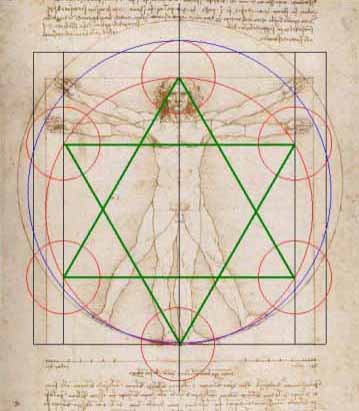

The Vitruvian Man is a drawing created by Leonardo da Vinci circa 1490. It is accompanied by notes based on the work of the architect Vitruvius. The drawing, which is in pen and ink on paper, depicts a male figure in two superimposed positions with his arms and legs apart and simultaneously inscribed in a circle and square. The drawing and text are sometimes called the Canon of Proportions or, less often, Proportions of Man.

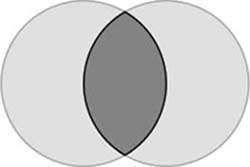
Vesica Piscis
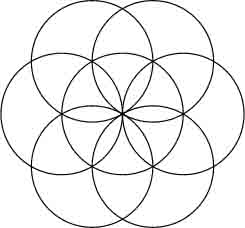
Flower of Life
Tree of Life - Qabbalah - Kabbalah
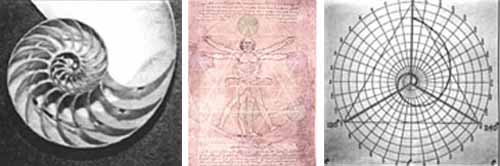
Sacred Geometry
When things come fun circle
The Human Equation: The brain works on binary code.
It's all an algorithm in the alchemy of time.


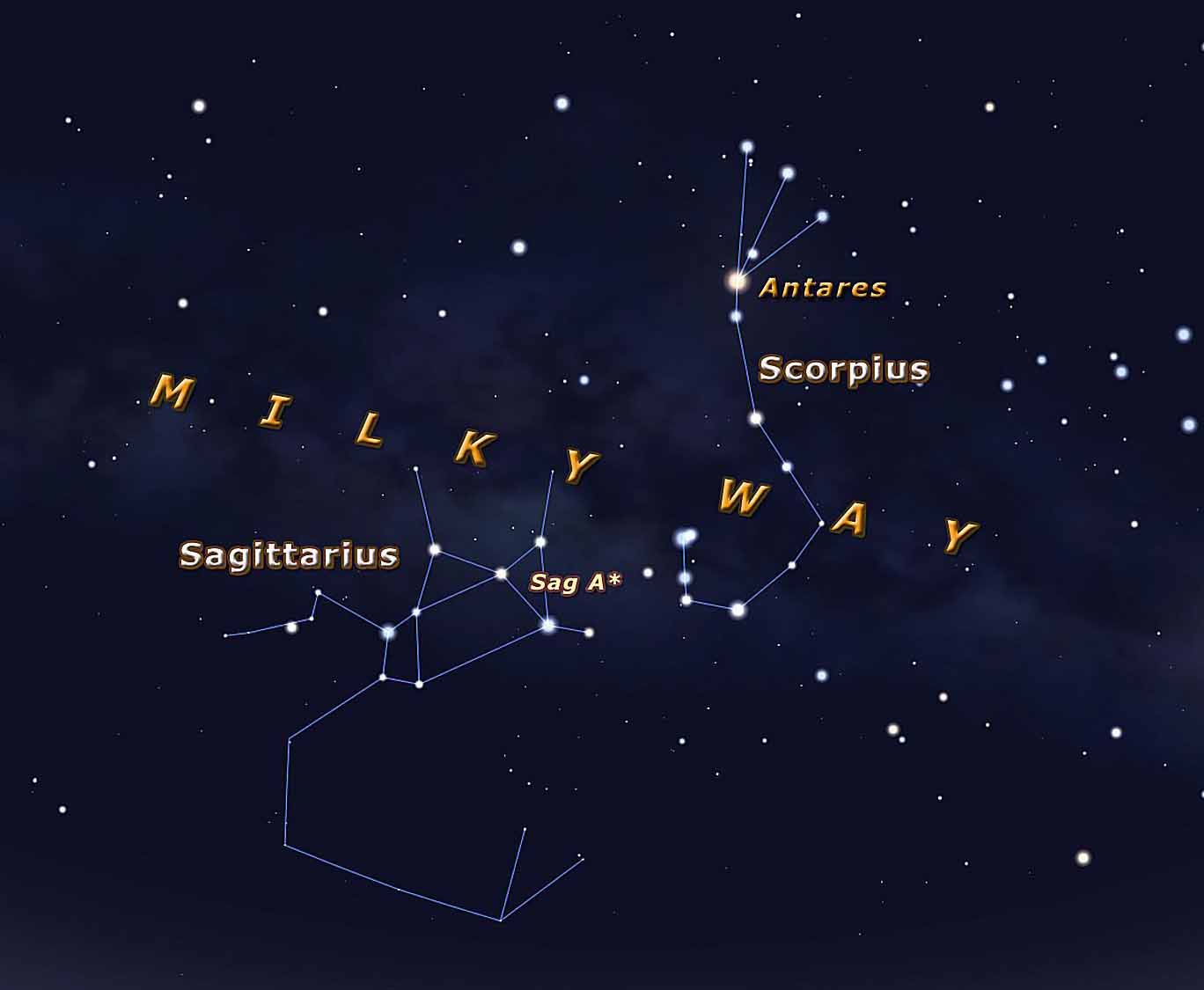
Sagittarius A* is a bright and very compact astronomical radio source at the Galactic Center of the Milky Way. Sagittarius A* is the location of a supermassive black hole, similar to massive objects at the centers of most, if not all, spiral and elliptical galaxies. On May 12, 2022, astronomers using the Event Horizon Telescope released a photograph of Sagittarius A*, confirming the object to contain a black hole. Continue reading
The center of the Milky Way Galaxy is sometimes referred to as the Ouroboros - the snake that eats its tail in the end or coming full circle - dark energy (Quintessence) - return through the shimmering black hole of creation.
In 2012 someone on Ancient Aliens linked it with the Mayan Calendar Prophecy about coming 'full circle' on December 21, 2012. In Numerology we find 12/21/12 or 12+21+12= 9= Endings. The concept was right but the date was wrong as time is an illusion. Our Simulation ends when the Fibonacci sequence reverts to zero. Currently it is at 0,1.
Suntelia Aion referred to the sun (light) rising out of the mouth of the ouroboros (aion) on the winter solstice December 21, 2012. Endings always are catastrophic as the grids collapse disappearing into the zero point of the Fibonacci sequence or the center of the black hole of creation. No matter where mythology, numerology, prophecy, or celestial messages take you - it all begins and ends with a shimmering black hole in the alchemy of time.

Sagittarius

Simulation Theory - Holographic Universe Theory
