M. C. Escher
Perception, Geometry, Thinking Outside the Box
Most of us are familiar with the work of M.C. Escher as a doorway to sacred geometry laced with metaphors and topics I have written about through the years. Everything goes to perception, but when do we become aware. At each phase of our experience here our perceptions vary from how we feel about people, situations, or simply the way we view the world.
Infants are able to detect the 'impossible objects' at early age EurekAlert - March 20, 2007
Is this about thinking outside the box?
These images are, of course, mere deceptions that result from our ability to create three-dimensional objects from two-dimensional images. An artist will use techniques such as shading, shadow, texture and the like to give his or her image a three-dimensional quality and sometimes, as in Escher's case, to confuse our ability to perceive them.
So when do we develop this ability to perceive coherence in three-dimensional objects? New York University perception researcher Sarah Shuwairi and her colleagues are now attempting to use this natural propensity to gaze at images of impossible objects to pinpoint when human infants develop the ability to perceive three-dimensional shape information from two-dimensional images.
To do this, Shuwairi enlisted 30 4-month-old infants to take part in a series of related experiments. With the help of their parents, the infant subjects sat in front of a computer screen that displayed alternating "possible" and "impossible" three-dimensional images. In the process, the researchers recorded how long the infants looked at each of the objects. As the reasoning goes, if the infants are sensitive to the visual features that give images a three-dimensional quality, they will inevitably gaze at the images that make no sense just as adults do; that is, they will stare at impossible objects longer.
The result was that infants looked significantly longer at impossible figures, suggesting that that as young as 4-months-old, humans have the ability to detect at least some three-dimensional features that give rise to the perception of object coherence.
Shuwairi explains that these findings, the first to document such abilities so early in development, "provide important insights into the development of mechanisms for processing pictorial depth cues that allow adults to extract 3D structure from pictures of objects." Ultimately, the implications of the research extend beyond the ability to be perplexed by visual impossibilities as researchers now have an additional tool to explain how infants develop an understanding of the physical world around them.
Remember when I was struggling with an expression that I thought was a truncated Dodecahedron (12). I may have confused it with 'stellated dodecahedron'. (see below)
M. C. Escher Website
M. C. Escher Images (Google) Great Metaphors
About M.C. Escher Wikipedia
Maurits Cornelis Escher (June 18, 1898 March 27, 1972) was a Dutch graphic artist known for his often mathematically inspired woodcuts, lithographs and mezzotints which feature impossible constructions, explorations of infinity, architecture, and tessellations.
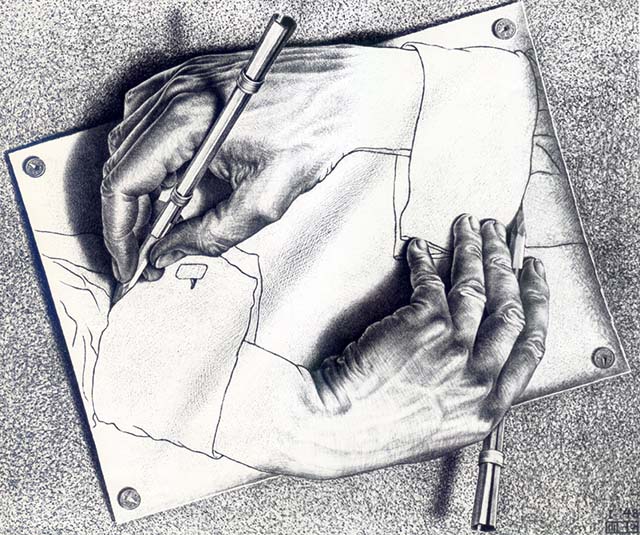
Escher's first print of an impossible reality was Still Life and Street, 1937. His artistic expression was created from images in his mind, rather than directly from observations and travels to other countries. Well known examples of his work also include Drawing Hands, a work in which two hands are shown, each drawing the other; Sky and Water, in which light plays on shadow to morph fish in water into birds in the sky; Ascending and Descending, in which lines of people ascend and descend stairs in an infinite loop, on a construction which is impossible to build and possible to draw only by taking advantage of quirks of perception and perspective.
He worked primarily in the media of lithographs and woodcuts, though the few mezzotints he made are considered to be masterpieces of the technique. In his graphic art, he portrayed mathematical relationships among shapes, figures and space. Additionally, he explored interlocking figures using black and white to enhance different dimensions. Integrated into his prints were mirror images of cones, spheres, cubes, rings, and spirals.
In addition to sketching landscape and nature in his early years, he also sketched insects, which frequently appeared in his later work. His first artistic work was completed in 1922, which featured eight human heads divided in different planes. Later in about 1924, he lost interest in "regular division" of planes, and turned to sketching landscapes in Italy with irregular perspectives that are impossible in natural form.
Although Escher did not have a mathematical training, his understanding of mathematics was largely visual and intuitive - Escher's work has a strong mathematical component, and more than a few of the worlds which he drew are built around impossible objects such as the Necker (impossible) cube and the Penrose triangle.
Many of Escher's works employed repeated tilings called tessellations. Escher's artwork is especially well-liked by mathematicians and scientists, who enjoy his use of polyhedra and geometric distortions. For example, in Gravity, multi-colored turtles poke their heads out of a stellated - dodecahedron.
The mathematical influence in his work emerged in about 1936, when he was journeying the Mediterranean with the Adria Shipping Company. Specifically, he became interested in order and symmetry. Escher described his journey through the Mediterranean as "the richest source of inspiration I have ever tapped." After his journey to the Alhambra, Escher tried to improve upon the art works of the Moors using geometric grids as the basis for his sketches, which he then overlaid with additional designs, mainly animals such as birds and lions.
His first study of mathematics, which would later lead to its incorporation into his art works, began with George Pólya's academic paper on plane symmetry groups sent to him by his brother Berend. This paper inspired him to learn the concept of the 17 wallpaper groups (plane symmetry groups). Utilizing this mathematical concept, Escher created periodic tilings with 43 colored drawings of different types of symmetry. From this point on he developed a mathematical approach to expressions of symmetry in his art works. Starting in 1937, he created woodcuts using the concept of the 17 plane symmetry groups.
In 1941, Escher wrote his first paper, now publicly recognized, called Regular Division of the Plane with Asymmetric Congruent Polygons, which detailed his mathematical approach to artwork creation. His intention in writing this was to aid himself in integrating mathematics into art. Escher is considered a research mathematician of his time because of his documentation with this paper. In it, he studied color based division, and developed a system of categorizing combinations of shape, color, and symmetrical properties. By studying these areas, he explored an area that later mathematicians labeled crystallography, an area of mathematics.
Around 1956, Escher explored the concept of representing infinity on a two-dimensional plane. Discussions with Canadian mathematician H.S.M. Coxeter inspired Escher¹s interest in hyperbolic tessellations, which are regular tilings of the hyperbolic plane. Escher¹s work Circle Limit I demonstrates this concept.
In 1995, Coxeter verified that Escher had achieved mathematical perfection in his etchings in a published paper. Coxeter wrote, "[Escher] got it absolutely right to the millimeter."
Escher later completed Circle Limit II, III and IV. These works continued to demonstrate his ability to create perfectly consistent mathematical designs. His works brought him fame: he was awarded the Knighthood of the Order of Orange Nassau in 1955. Subsequently he regularly designed art for dignitaries around the world.
In 1958, he published a paper called Regular Division of the Plane, in which he described the systematic buildup of mathematical designs in his artworks. He emphasized, "[Mathematicians] have opened the gate leading to an extensive domain."
Overall, his early love of Roman and Italian landscapes and of nature led to his interest in regular division of a plane. He worked in the media of woodcuts, lithographs, and mezzotints. In his lifetime he created over 150 colored works utilizing the concept of regular division of a plane. Other mathematical principles evidenced in his works include the superposition of a hyperbolic plane on a fixed 2-dimensional plane, and the incorporation of three-dimensional objects such as spheres, columns, and cubes into his works. For example, in a print called "Reptiles," he combined two and three-dimensional images. In one of his papers, Escher emphasized the importance of dimensionality and described himself as "irritated" by flat shapes: "I make them come out of the plane."
Escher also studied the mathematical concepts of topology. Escher learned additional concepts in mathematics from British mathematician Roger Penrose. From the new knowledge he created Waterfall and Up and Down, featuring irregular perspectives similar to the concept of the Möbius strip; Möbius himself being a mathematician who studied topology.
Escher printed Metamorphosis I in 1937, which was a beginning part of a series of designs that told a story through the use of pictures. These works demonstrated a culmination of Escher¹s skills to incorporate mathematics into art. In Metamorphosis I, he transformed convex polygons into regular patterns in a plane to form a human motif. This effect symbolizes his change of interest from landscape and nature to regular division of a plane.
One of his most notable works is the piece Metamorphosis III, which is wide enough to cover all the walls in a room, and then loop back onto itself. After 1953, Escher became a lecturer to many organizations. A planned series of lectures in North America in 1962 was cancelled due to illness, but the illustrations and text for the lectures, written out in full by Escher, was later published as part of the book Escher on Escher.
In July of 1969, he finished his last work before his death, a woodcut called Snakes. It features etchings of patterns that fade to infinity both to the center and the edge of a circle. Snakes transverse the circle and the patterns in it, with their heads sticking out of the circle.
ALPHABETICAL INDEX OF ALL FILES
CRYSTALINKS MAILING LIST, NEWSLETTER, UPDATES