

A black hole is a region of spacetime from which gravity prevents anything, including light, from escaping. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole, there is a mathematically defined surface called an event horizon that marks the point of no return. The hole is called "black" because it absorbs all the light that hits the horizon, reflecting nothing, just like a perfect black body in thermodynamics.
Quantum field theory in curved spacetime predicts that event horizons emit radiation like a black body with a finite temperature. This temperature is inversely proportional to the mass of the black hole, making it difficult to observe this radiation for black holes of stellar mass or greater.
Objects whose gravity fields are too strong for light to escape were first considered in the 18th century by John Michell and Pierre-Simon Laplace. The first modern solution of general relativity that would characterize a black hole was found by Karl Schwarzschild in 1916, although its interpretation as a region of space from which nothing can escape was first published by David Finkelstein in 1958. Long considered a mathematical curiosity, it was during the 1960s that theoretical work showed black holes were a generic prediction of general relativity. The discovery of neutron stars sparked interest in gravitationally collapsed compact objects as a possible astrophysical reality.
Black holes of stellar mass are expected to form when very massive stars collapse at the end of their life cycle. After a black hole has formed it can continue to grow by absorbing mass from its surroundings. By absorbing other stars and merging with other black holes, supermassive black holes of millions of solar masses may form. There is general consensus that supermassive black holes exist in the centers of most galaxies.
Despite its invisible interior, the presence of a black hole can be inferred through its interaction with other matter and with electromagnetic radiation such as light. Matter falling onto a black hole can form an accretion disk heated by friction, forming some of the brightest objects in the universe. If there are other stars orbiting a black hole, their orbit can be used to determine its mass and location. These data can be used to exclude possible alternatives (such as neutron stars). In this way, astronomers have identified numerous stellar black hole candidates in binary systems, and established that the core of our Milky Way galaxy contains a supermassive black hole of about 4.3 million solar masses. Continue reading

A quasar is an extremely luminous active galactic nucleus (AGN). It is sometimes known as a quasi-stellar object, abbreviated QSO. The emission from an AGN is powered by a supermassive black hole with a mass ranging from millions to tens of billions of solar masses, surrounded by a gaseous accretion disc. Gas in the disc falling towards the black hole heats up because of friction and releases energy in the form of electromagnetic radiation. The radiant energy of quasars is enormous; the most powerful quasars have luminosities thousands of times greater than that of a galaxy such as the Milky Way. Usually, quasars are categorized as a subclass of the more general category of AGN. The redshifts of quasars are of cosmological origin. More than a million quasars have been found, with the nearest known being about 600 million light-years away from Earth. Continue reading

Starlight From Quasar Galaxies Has Been Detected at The Dawn of The Universe Science Alert - June 29, 2023
With combined data from the Subaru Telescope in Hawaii and the James Webb Space Telescope, a large international team has been able to probe two quasar galaxies in the early Universe to learn more about this mysterious time in the history of everything.

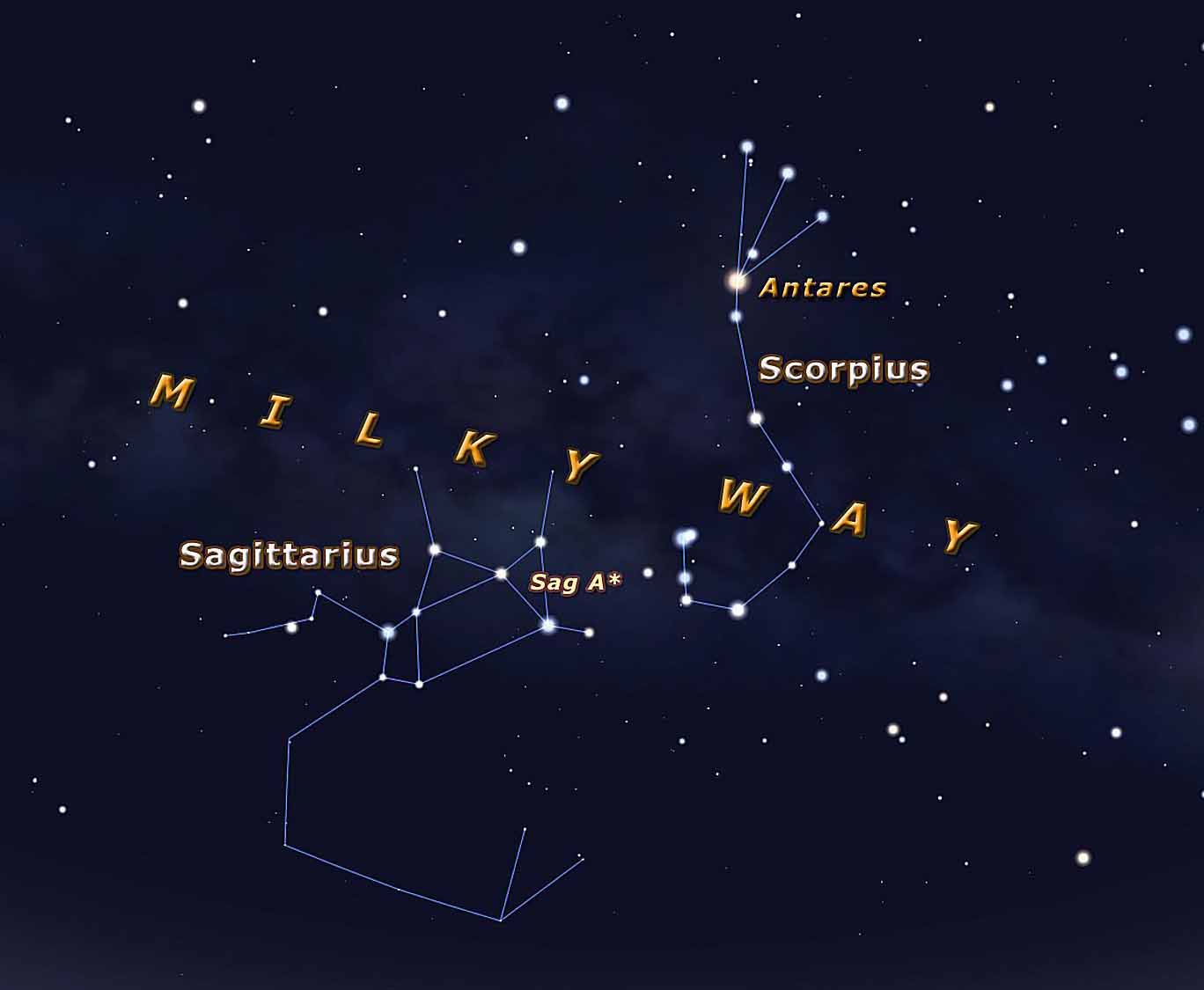
Sagittarius A* is a bright and very compact astronomical radio source at the Galactic Center of the Milky Way. Sagittarius A* is the location of a supermassive black hole, similar to massive objects at the centers of most, if not all, spiral and elliptical galaxies. On May 12, 2022, astronomers using the Event Horizon Telescope released a photograph of Sagittarius A*, confirming the object to contain a black hole. Continue reading
The Human Equation: The brain works on binary code.
It's all an algorithm in the alchemy of time.

The center of the Milky Way Galaxy is sometimes referred to as the Ouroboros - the snake that eats its tail in the end or coming full circle - dark energy (Quintessence) - return through the shimmering black hole of creation.
In 2012 someone on Ancient Aliens linked it with the Mayan Calendar Prophecy about coming 'full circle' on December 21, 2012. In Numerology we find 12/21/12 or 12+21+12= 9= Endings. The concept was right but the date was wrong as time is an illusion. Our Simulation ends when the Fibonacci sequence reverts to zero. Currently it is at 0,1.
Suntelia Aion referred to the sun (light) rising out of the mouth of the ouroboros (aion) on the winter solstice December 21, 2012. Endings always are catastrophic as the grids collapse disappearing into the zero point of the Fibonacci sequence or the center of the black hole of creation. No matter where mythology, numerology, prophecy, or celestial messages take you - it all begins and ends with a shimmering black hole in the alchemy of time.

Sagittarius

Simulation Theory - Holographic Universe Theory

For the first time, scientists have watched a black hole twist spacetime itself - just as Einstein predicted a century ago. Science Daily - December 19, 2025

The universe has delivered a rare breakthrough for researchers chasing one of the hardest effects to catch in the night sky. Scientists describe the first observations of a spiraling swirl in spacetime linked to a fast spinning black hole.
Scientists Finally Explain Mysterious Impossible Merger of Two Massive Black Holes SciTech Daily - December 8, 2025

A detailed suite of simulations conducted by astrophysicists showed that magnetic fields can produce black holes with masses that were previously believed to be mostly unattainable.
Astronomers Discover a Star That Breaks the Rules Orbiting a Silent Black Hole SciTech Daily - November 26, 2025
Astronomers have uncovered clues to a red giant’s chaotic past by detecting subtle stellar vibrations that hint at a long-ago collision and an unexpectedly rapid spin.
Scientists Finally Hear Black Holes Ring, Confirming Hawking's Famous Prediction Science Daily - October 24, 2025

Rogue black hole shocks astronomers with record radio blast Science Daily - October 18, 2025

A rogue black hole shredded a star and unleashed record-fast radio flares, rewriting what we thought we knew about these cosmic beasts.
Groundbreaking image shows two black holes orbiting each other for first time Live Science - October 10, 2025

For the first time ever, astronomers have imaged two black holes orbiting each other, finally offering visual proof for the existence of black hole pairs.
The James Webb telescope may have discovered a brand new class of cosmic object: the black hole star Live Science - September 24, 2025

A tiny particle that smashed into Earth with a record-shattering energy of 220 petaelectronvolts could be the last scream of an evaporating black hole.
Gravitational wave analysis confirms theory of merging black holes PhysOrg - September 14, 2025

Ten years after scientists first detected gravitational waves emerging from two colliding black holes a research team has recorded a signal from a nearly identical black hole collision.
'Mysterious Giant' Hints at The First Detection of a Black Hole Trinary Science Alert - August 17, 2025

A strange signal in the background hum created by a merger between two black holes could be the first ever detection of a system of three stellar-mass black holes locked in a gravitational waltz.
Meet the universe's earliest confirmed black hole: A monster at the dawn of time PhysOrg - August 6, 2025

An international team of astronomers has identified the most distant black hole ever confirmed. It and the galaxy it calls home, CAPERS-LRD-z9, are present 500 million years after the Big Bang. That places it 13.3 billion years into the past, when our universe was just 3% of its current age. As such, it provides a unique opportunity to study the structure and evolution of this enigmatic period.
Meet 'lite intermediate black holes,' the supermassive black hole's smaller, much more mysterious cousin PhysOrg - August 4, 2025

Black holes are massive, strange and incredibly powerful astronomical objects. Scientists know that supermassive black holes reside in the centers of most galaxies. And they understand how certain stars form the comparatively smaller stellar mass black holes once they reach the end of their life. Understanding how the smaller stellar mass black holes could form the supermassive black holes helps astronomers learn about how the universe grows and evolves. But there's an open question in black hole research: What about black holes with masses in between? These are much harder to find than their stellar and supermassive peers, in size range of a few hundred to a few hundred thousand times the mass of the sun.
Black holes don't just swallow light, they sing. And we just learned the tune Science Daily - August 2, 2025
Using a powerful mathematical tool, scientists have unveiled the intricate "ringing" of black holes, unlocking patterns missed for decades and laying the groundwork for sharper gravitational wave measurements. A new method exposes the hidden spirals in black hole vibrations, reshaping how we hear and understand their cosmic signals. Black holes embody the ultimate abyss. They are the most powerful sources of gravity in the universe, capable of dramatically distorting space and time around them. When disturbed, they begin to "ring" in a distinctive pattern known as quasinormal modes: ripples in space-time that produce detectable gravitational waves.
Some of the brightest sources of light in the sky come from the regions around black holes in the centers of galaxies PhysOrg - May 1, 2025

Black holes are regions of space that have so much gravity that nothing - not light, not particles, nada - can escape. Most galaxies have supermassive black holes at their centers, and these black holes are hundreds of thousands to billions of times the mass of our sun.
The Mysterious History of a Black Hole Has Been Decoded by Scientists Science Alert - April 4, 2025

One of the common misconceptions about black holes is that they devour not only matter, but also the history of that matter. So when a black hole forms, you can only guess how it came to be.
Is our universe trapped inside a black hole? This James Webb Space Telescope discovery might blow your mind Live Science - March 17, 2025
The simplest explanation of the rotating universe is that the universe was born inside a rotating black hole. That explanation agrees with theories such as black hole cosmology, which postulates that the entire universe is within the interior of a black hole. Simulation Theory
Einstein's theory of general relativity suggests that the "memory" of ancient events, such as black hole mergers, may be etched into the fabric of space-time by gravitational waves Live Science - March 6, 2025
New research shows how this theory of gravitational memory could finally be proven. The researchers suggest that the cosmic microwave background - a faint glow left over from the Big Bang - might carry the signatures of powerful gravitational waves from distant black hole mergers. Studying these signals could not only confirm Einstein's prediction but also shed light on some of the most energetic events in the universe's history.
Supermassive black hole spotted 12.9 billion light-years from Earth - and it's shooting a beam of energy right at us Live Science - January 16, 2025

The newly discovered "blazar," which has a mass equal to 700 million suns, is the oldest of its kind ever seen and changes what we know about the early universe. Astronomers have discovered a supermassive black hole that's shooting a giant energy beam directly at Earth. The cosmic juggernaut, which is about as massive as 700 million suns, is taking aim at us from a galaxy in the early universe, up to 800 million years after the Big Bang - making this the most distant "blazar" ever found.
Scientists Reveal The Shape of a Black Hole's Corona For The Very First Time

According to our understanding of black hole dynamics black holes should also have a corona. And like the Sun's corona, it is usually difficult to observe. Now a study in The Astrophysical Journal has made observations of this elusive region. For an active black hole, it's generally thought that there is a donut-shaped torus of gas and dust surrounding the black hole, in which there is an accretion disk of heated material aligned along the rotational plane of the black hole.
Black Holes Are Sending Signals - Astrophysicists' Groundbreaking Method for Decoding Them SciTech Daily - November 13, 2024
Astrophysicists have developed a method to detect light echoes from black holes, potentially revolutionizing the measurement of their masses and spins.
A Star Vanished And Was Mysteriously Replaced by a Black Hole Science Alert - November 11, 2024

Massive stars about eight times more massive than the Sun explode as supernovae at the end of their lives. The explosions, which leave behind a black hole or a neutron star, are so energetic they can outshine their host galaxies for months. However, astronomers appear to have spotted a massive star that skipped the explosion and turned directly into a black hole.
Extraordinary 'Trinary' Black Hole System Is The First of Its Kind Ever Found Science Alert - October 25, 2024

In the constellation of Cygnus, some 7,800 light-years from Earth, lurks a real space oddity. There, a black hole in a system named V404 Cygni repeatedly engages in behavior that has simultaneously baffled and delighted scientists.
How Holographic Dark Energy Could Lead To The End Of The Universe IFL Science - October 23, 2024
A team looking into dark energy and the holographic principle have modeled what the end of the universe may look like, assuming that the universe is a hologram after all.
Simulation Theory - Holographic Universe
Tiny Black Holes Could Lurk Inside Asteroids, Moons, or Even Planets Like Ours Science Alert - October 7, 2024

Small primordial black holes (PBHs) are one of the hot topics in astronomy and cosmology today. These hypothetical black holes are believed to have formed soon after the Big Bang, resulting from pockets of subatomic matter so dense that they underwent gravitational collapse.
This Mysterious Black Hole at The Dawn of Time Weighs a Billion Suns Science Alert - June 30, 2024

A black hole discovered lurking in the Cosmic Dawn is just way too big to easily explain. Sitting at the center of a galaxy called J1120+0641, it tips the scales at well over a billion Suns' worth of mass.
Supermassive Black Hole Seen Waking Up In Real Time In World First IFL Science - June 18, 2024
Supermassive black holes can be quiet or active. In their active state, they are feeding. Some brief events could be an unfortunate star passing too close – these brightenings last at most a few hundred days. But the supermassive black holes that get to be called active galactic nuclei, or AGNs, are the ones releasing so much light that they are about to outshine their host galaxies for a very long time. And this is what astronomers are seeing here.
Physicists Finally Confirm Einstein's Stunning Prediction About Black Holes Science Alert - May 20, 2024

The detailed mechanics of how matter falls down onto a black hole from outside the event horizon have been revealed. As predicted by Einstein's theory of gravity, there's a point at which material stops circling the black hole and falls straight down, plunging precipitously beyond the point of no return.
Why Some Physicists Think We Are Living Inside A Black Hole IFL Science - May 8, 2024
Black holes are strange objects which (though we have learned plenty about them) confound our understanding of physics. In an attempt to reconcile some of the paradoxes discovered when studying them, physicists have proposed stranger hypotheses still, with one suggesting that they imply we live in a holographic universe, where all of what we see and perceive is in fact encoded at our universe's boundary, a 3D (plus time) representation of a two-dimensional (plus time) universe. Further than that, some have suggested that it could imply that our universe is within a black hole of a larger universe.
Most massive stellar black hole in the Milky Way discovered 'extremely close' to Earth Live Science - May 7, 2024
Astronomers have found the most massive stellar-mass black hole ever discovered in our galaxy - and it's lurking "extremely close" to Earth, according to new research. The black hole, named Gaia BH3, is 33 times more massive than our sun. Cygnus X-1, the next-biggest stellar black hole known in our galaxy, weighs only 21 solar masses. The newfound black hole is located roughly 2,000 light-years away in the constellation Aquila, making it the second-closest known black hole to Earth.

Record-Breaking Stellar Black Hole Found Lurking Close to Earth 1,924 light-years from the Solar System, in the constellation of Aquila Science Alert - April 17, 2024
Named Gaia BH3, or BH3, the object is the most massive stellar-mass black hole we've ever spotted in the Milky Way, clocking in at a hefty 33 times the mass of the Sun. It's the second-closest black hole we've found to our home world, and it's just hanging out, quietly in space, minding its own black hole business. The only reason we know it's there is because it's in a binary orbit with a companion star whose motion can't be explained any other way.
NASA's Stunning New Simulation Sends You Diving Into a Black Hole Science Alert - May 7, 2024
Jump Into A Black Hole With NASA's Incredible New Visualization IFL Science - May 7, 2024
This takes you to Simulation Theory
Can Information Escape Black Holes? Physicists Sure Hope So IFL Science - May 3, 2024
The black hole information paradox is one of those physics problems that can keep scientists up at night. It strikes at the heart of one of the crucial problems in modern physics: the fact that we can’t reconcile general relativity and quantum mechanics. And it is all black holes' fault. Both quantum mechanics and general relativity are pinnacles of human knowledge and ingenuity. Truly, we should be very proud of ourselves and how well we understand the universe. Still, the two do not work together very well, and when it comes to certain extreme objects or events, they break down - and that is a big problem. The black hole information paradox is one of these cases.
Bubble-Like 'Stars Within Stars' Could Explain Black Hole Weirdness Science Alert - February 20, 2024

Once hypothetical monsters born in a tangled nest of Einstein's general theory of relativity, black holes are now recognized as bona fide celestial objects as real as stars, moons, and galaxies.
James Webb telescope discovers the oldest, most distant black hole in the universe Live Science - January 18, 2024
The James Webb Space Telescope (JWST) has spotted the oldest black hole ever seen, an ancient monster with the mass of 1.6 million suns lurking 13 billion years in the universe's past. The James Webb Space Telescope, whose cameras enable it to look back in time to our universe's beginnings, spotted the supermassive black hole at the center of the infant galaxy GN-z11 just 440 million years after the universe began. And the space-time rupture isn't alone, it's one of countless black holes that gorged themselves to terrifying scales during the cosmic dawn - the period about 100 million years after the Big Bang when the young universe began glowing for a billion years.
We Now Have Precise Math To Describe How Black Holes Reflect Our Universe Science Alert - December 14, 2023

Astronomers developed a set of equations that can precisely describe the reflections of the Universe that appear in the warped light around a black hole. The proximity of each reflection is dependent on the angle of observation with respect to the black hole, and the rate of the black hole's spin.
Oldest Black Hole Discovered Dating To Just 470 Million Years After Big Bang Science Alert - November 6, 2023
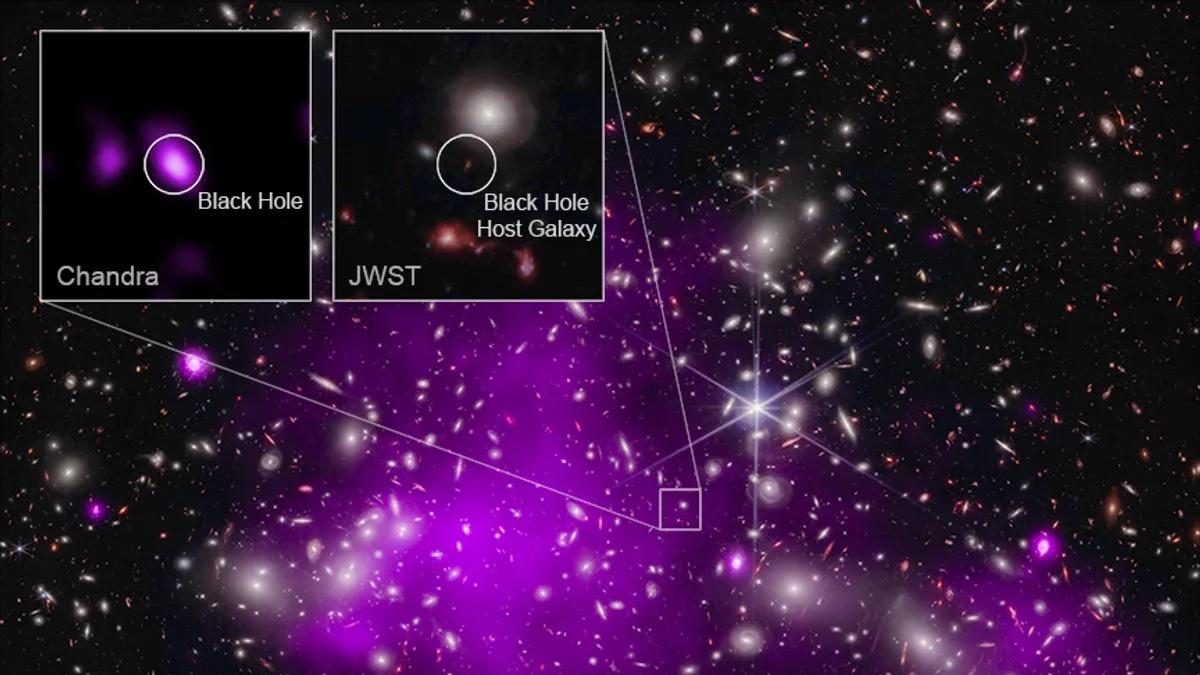
A supermassive black hole smack-bang in the Cosmic Dawn has broken the record for the earliest black hole we've ever seen. It's been spotted in a galaxy known as UHZ1, just 470 million years after the Big Bang, a time period when the Universe was still just a baby. In fact, it's so early in the Universe that the black hole is at a stage of development we've never seen before - it's of a similar mass to the host galaxy that is growing around it.
Milky Way's Black Hole Is Spinning at Near Maximum, Scientists Say Science Alert - November 1, 2023

It's Official: The M87 Black Hole Is Spinning Science Alert - September 29, 2023 Science Alert - September 29, 2023

The black hole at M87’s center is 6.5 billion times larger than the Sun. To capture the first image of a black hole, researchers had to build a telescope as big as Earth by stitching together data from observatories around the globe.
Newly discovered black hole speed limit hints at new laws of physics Live Science - August 23, 2023
When supermassive black holes barrel toward collision, they can reach speeds of up to 1/10th the speed of light, new research suggests. Researchers have identified a new speed limit for the universe’s most extreme collisions. The maximum possible recoil velocity for colliding black holes exceeds a whopping 63 million mph (102 million km/h) - about one-tenth the speed of light. This peak occurs when the collision conditions are at the tipping point between the two black holes either merging together or scattering apart as they approach each other.
Gargantuan black hole 'switches on,' becoming one of the brightest objects ever seen Live Science - July 8, 2023
The Earliest Supermassive Black Hole Ever Found Has Been Identified Science Alert - July 6, 2023
An object lurking in the foggy dawn of the Universe has given astronomers a big surprise. Observations collected through the James Webb Space Telescope have revealed an active supermassive black hole 9 million times the mass of the Sun - one that is actively growing as it slurps up matter from the space around it.
Could Earth be inside a black hole? Live Science - June 18, 2023

There's one way Earth might have ended up in the belly of a black hole: It could have formed there. Various theories discussed.
Black hole evaporation: Theoretical study proves Stephen Hawking partially correct PhysOrg - June 2, 2023
Everything evaporates. New theoretical research by Michael Wondrak, Walter van Suijlekom and Heino Falcke of Radboud University has shown that Stephen Hawking was right about black holes, although not completely. Due to Hawking radiation, black holes will eventually evaporate, but the event horizon is not as crucial as had been believed. Gravity and the curvature of spacetime cause this radiation too. This means that all large objects in the universe, like the remnants of stars, will eventually evaporate.
Wild Study Shows Everything in The Universe Will Eventually Evaporate Science Alert - June 2, 2023

According to a famous theory by Stephen Hawking, black holes evaporate over time, gradually losing mass in the form of a strange kind of radiation as the event horizon plays havoc with surrounding quantum fields. But it turns out that the dramatic cliff of an event horizon may not be as critical to this process after all. According to new research by astrophysicists in the Netherlands, a steep enough slope in the curvature of space-time could do the same thing. This means Hawking radiation, or something very similar to it, may not be limited to black holes. It could be everywhere, meaning that the Universe is very slowly evaporating before our very eyes.
Researchers Argue Black Holes Will Destroy All Quantum States Wired - April 24, 2023
Physicists Simulated a Black Hole in The Lab, And Then It Started to Glow Science Alert - April 6, 2023

A synthetic analog of a black hole could tell us a thing or two about an elusive radiation theoretically emitted by the real thing. Using a chain of atoms in single-file to simulate the event horizon of a black hole, a team of physicists observed the equivalent of what we call Hawking radiation - particles born from disturbances in the quantum fluctuations caused by the black hole's break in spacetime. This, they say, could help resolve the tension between two currently irreconcilable frameworks for describing the Universe: the general theory of relativity, which describes the behavior of gravity as a continuous field known as spacetime; and quantum mechanics, which describes the behavior of discrete particles using the mathematics of probability.
Astronomers Studied More Than 5,000 Black Holes to Figure Out Why They Twinkle Science Alert - February 3, 2023
Despite their famous blackness, some black holes are quite visible. The gas and stars these galactic vacuums devour are sucked into a glowing disc before their one-way trip into the hole, and these discs can shine more brightly than entire galaxies.
Elusive 'Buchdahl stars' are black holes without event horizons. These hypothetical stars are the densest objects in the universe that can exist without becoming full-fledged black holes Live Science - January 16, 2023
An elusive object in space has posed a riddle for scientists. It looks like a black hole. It acts like a black hole. It may even smell like a black hole. It has one crucial difference: It has no event horizon, meaning that you can escape its gravitational clutches if you try hard enough. But no one has ever observed one, leading to questions about whether the mysterious objects actually exist. Now, a physicist may have uncovered a new property of Buchdahl stars that could help to answer that.
Scientists created a mini black hole and it started radiating SciTech - December 1, 2022
Scientists have managed to simulate their very own black hole in their lab and witnessed how it began to glow. The black hole event horizon was created by a team of physicists from the University of Amsterdam, who used a chain of atoms in a single file to gain further understanding about the behavior of a black hole. Its creation managed to prove Stephen Hawking's theory from 1974 where the black hole emitted a rare form of radiation.
Mysterious bright flash is a black hole jet pointing straight toward Earth, astronomers say Science Daily - December 1, 2022
Astronomers have determined the source of an incredibly bright X-ray, optical and radio signal appearing from halfway across the Universe.
Mysteriously bright flash is a black hole jet pointing straight toward Earth, astronomers say PhysOrg - December 1 , 2022

Earlier this year, astronomers were keeping tabs on data from the Zwicky Transient Facility, an all-sky survey based at the Palomar Observatory in California, when they detected an extraordinary flash in a part of the sky where no such light had been observed the night before. From a rough calculation, the flash appeared to give off more light than 1,000 trillion suns.
Two Black Holes Met by Chance, And It Created Something Never Seen Before Science Alert - November 24, 2022
The ripples in space-time generated by colliding black holes have taught us a lot about these enigmatic objects. These gravitational waves encode information about black holes: their masses, the shape of their inward spiral towards each other, their spins, and their orientations.
'Potentially Hazardous' Monster Asteroid Is The Largest Seen in Years Science Alert - October 31, 2022

Astronomers developed a set of equations that can precisely describe the reflections of the Universe that appear in the warped light around a black hole. The proximity of each reflection is dependent on the angle of observation with respect to the black hole, and the rate of the black hole's spin.
NASA Recorded The Sounds From a Black Hole Science Alert - August 22, 2022
The fastest-growing black hole of the last 9 billion years has been discovered PhysOrg - June 15, 2022
The fastest-growing black hole of the last 9 billion years has been discovered by an international team led by astronomers. The black hole consumes the equivalent of one Earth every second and shines 7,000 times brighter than all the light from our own galaxy, making it visible to well-equipped backyard astronomers. The black hole has the mass of three billion suns. Others of a comparable size stopped growing so quickly billions of years ago.
A Rogue Black Hole Roaming Our Galaxy May Have Just Been Confirmed Science Alert - June 14, 2022

The first detection of what appears to be a rogue black hole drifting through the Milky Way, revealed earlier this year, just got important validation. A second team of scientists, conducting a separate, independent analysis, has reached almost the same finding, adding weight to the idea that we've potentially identified a rogue black hole wandering the galaxy.
Astronomers may have detected a 'dark' free-floating black hole Science Daily - June 13, 2022

Astronomers have discovered what may be a free-floating black hole by observing the brightening of a more distant star as its light was distorted by the object's strong gravitational field -- so-called gravitational microlensing. Black holes, by their nature, are invisible unless part of a stellar binary or surrounded by an accretion disk. Most stellar-sized black holes aren't, but astronomers have been searching for them through gravitational microlensing events, where the black hole brightens and distorts light from stars toward the galactic center. A UC Berkeley-led team may have found the first free-floating black hole, though more data is needed to rule out a neutron star. If, as astronomers believe, the death of large stars leave behind black holes, there should be hundreds of millions of them scattered throughout the Milky Way galaxy. The problem is, isolated black holes are invisible.
We May Have Caught a Supermassive Black Hole Flipping Its Entire Magnetic Field Science Alert - May 12, 2022
In a pair of merging supermassive black holes, a new method for measuring the void PhysOrg - May 12, 2022
Three years ago, the first ever image of a black hole stunned the world. A black pit of nothingness enclosed by a fiery ring of light. That iconic image of the black hole at the center of galaxy Messier 87 came into focus thanks to the Event Horizon Telescope, a global network of synchronized radio dishes acting as one giant telescope. Now, a pair of Columbia researchers have devised a potentially easier way of gazing into the abyss.
These Eerie Wails Are a Real Sound Wave From a Supermassive Black Hole Science Alert - May 9, 2022

We might not be able to hear sound in space, but that doesn't mean there isn't any. In 2003, astronomers detected something truly astonishing: acoustic waves propagating through the gas surrounding a supermassive black hole, 250 million light-years away.
Death Spiral: A Black Hole Spins on Its Side - Completely Unexpected SciTech - February 26, 2022
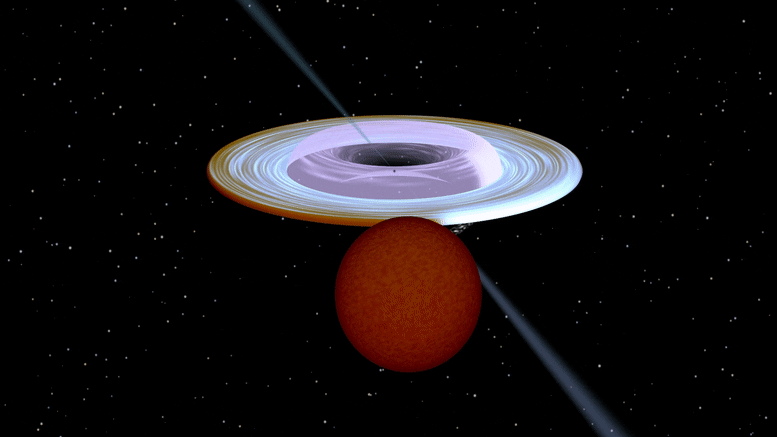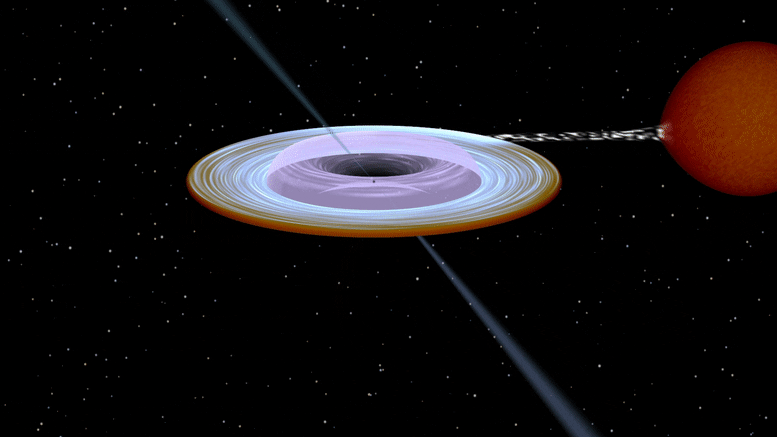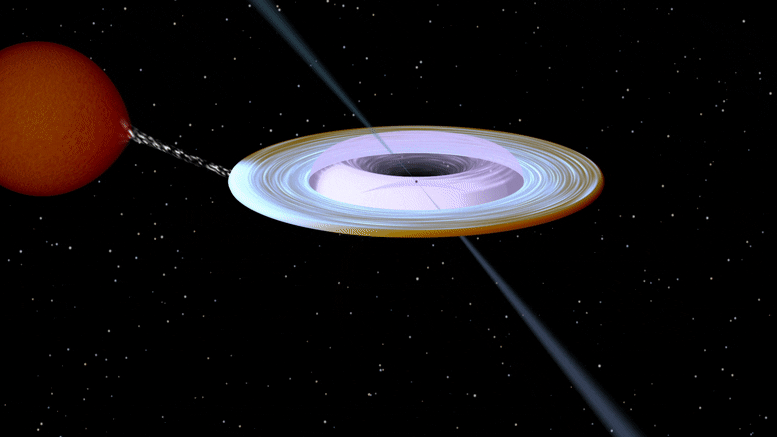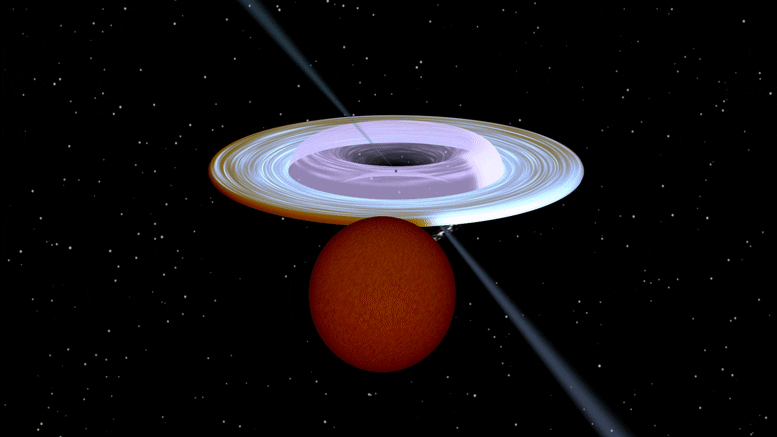
Researchers from the University of Turku, Finland, found that the axis of rotation of a black hole in a binary system is tilted more than 40 degrees relative to the axis of stellar orbit. The finding challenges current theoretical models of black hole formation.
Colossal black holes locked in dance at heart of galaxy PhysOrg - February 23, 2022
Locked in an epic cosmic waltz 9 billion light years away, two supermassive black holes appear to be orbiting around each other every two years. The two giant bodies each have masses that are hundreds of millions of times larger than that of our sun, and the objects are separated by a distance roughly 50 times that which separates our sun and Pluto. When the pair merge in roughly 10,000 years, the titanic collision is expected to shake space and time itself, sending gravitational waves across the universe.
First ever free-floating black hole found roaming through interstellar space PhysOrg - February 4, 2022
An international team of researchers has confirmed that a possible microlensing event witnessed in 2011 was due to the presence of a free-floating black hole roaming through interstellar space - the first of its kind ever observed.
Einstein's theory of general relativity is proven after scientists see light coming from behind a black hole for the first time ever Daily Mail - July 28, 2021
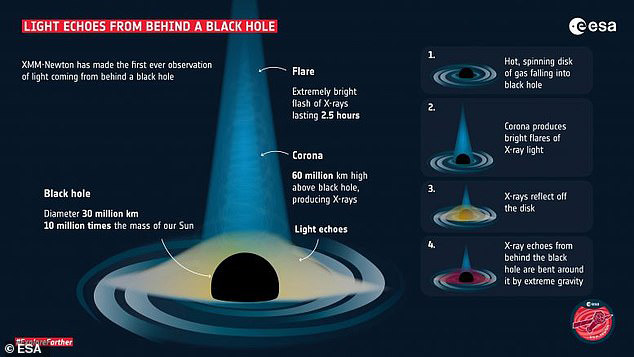
The scenario was predicted by Einstein's theory, which determined that massive objects cause a distortion in space-time, which is felt as gravity. Roger Blandford, a co-author of the research, published in Nature, said: 'Fifty years ago, when astrophysicists starting speculating about how the magnetic field might behave close to a black hole, they had no idea that one day we might have the techniques to observe this directly and see Einstein's general theory of relativity in action.' While conducting the research, Stanford University astrophysicist Dan Wilkins observed a series of bright flares of X-rays and then the telescopes recorded something unexpected: additional flashes of X-rays that were smaller, later and of different 'colors' than the bright flares.
Warped Light Emerging From Behind a Black Hole Has Been Detected For The First Time Science Alert - July 28, 2021

So extreme is the magnetic and gravitational environment around a black hole that we should see light bend around it and be reflected back at the viewer from behind the black hole - at least, per the theoretical predictions of Einstein's general relativity. Now, for the first time, astronomers have directly detected this reflected light, in the form of X-ray echoes from a supermassive black hole 800 million light-years away, in a galaxy called I Zwicky 1 (I Zw 1). This finally confirms Einstein's prediction, and sheds further light on the darkest objects in the Universe.
Variable emission from the Milky Way's supermassive black hole PhysOrg - June 12, 2021
At the center of our Milky Way lies a supermassive black hole (SMBH) called Sagittarius A* (SgrA*). Supermassive black holes reside at the centers of most galaxies, and when they actively accrete gas and dust onto their surrounding hot disks and environments, they radiate across the electromagnetic spectrum. The mass of SgrA* is about 4 million solar masses, much smaller than the billions of solar-mass SMBHs seen in some galaxies. However, it is relatively close by, only about 25,000 light-years distant, and this proximity provides astronomers with unique opportunities to probe the properties of SMBHs.
Sag A* has been monitored at radio wavelengths since its discovery in the 1950s. Variability was first reported in the radio in 1984, and subsequent infrared, submillimeter, and X-ray observations confirmed variability and found that it often flares. Monitoring programs have concluded that on average Sgr A* is accreting material at a very low rate, only a few hundredths of an Earth mass per year. The fascination with SgrA*'s variability has a practical diagnostic reason, too: Changes in emission are a measure of the dimensions of the region, set by the time for light to travel across it. Flares have been measured that doubled in strength in less than 47 seconds, for example, a time that corresponds to a distance about as small as this black hole's fundamental event horizon size (light cannot escape from within this boundary). These conclusions are in agreement with size inferences made with radio and near infrared interferometry.
A Gamma-Ray Burst Just Revealed a 'Goldilocks' Black Hole in The Early Universe nbsp; Science Alert - March 30, 2021
Scientists have reported the discovery of a rare, medium-sized black hole that may help answer one of the more tantalizing questions in astronomy: how do their supermassive counterparts come into being?
New study suggests supermassive black holes could form from dark matter Science Daily - February 25, 2021

A new theoretical study has proposed a novel mechanism for the creation of supermassive black holes from dark matter. The international team find that rather than the conventional formation scenarios involving 'normal' matter, supermassive black holes could instead form directly from dark matter in high density regions in the centers of galaxies. The result has key implications for cosmology in the early Universe.
New study suggests supermassive black holes could form from dark matter PhysOrg - February 25, 2021
A new theoretical study has proposed a novel mechanism for the creation of supermassive black holes from dark matter. The international team find that rather than the conventional formation scenarios involving 'normal' matter, supermassive black holes could instead form directly from dark matter in high density regions in the centers of galaxies. Exactly how supermassive black holes initially formed is one of the biggest problems in the study of galaxy evolution today. Supermassive black holes have been observed as early as 800 million years after the Big Bang, and how they could grow so quickly remains unexplained.
Swirling Vortex of Bathtub Water Reveals an Elusive Mechanism of Black Hole Physics Science Alert - February 4, 2021
When a black hole is active, we tend to focus on the effect it has on the material it's slurping up. It makes sense to do so; black holes themselves are difficult to probe. But the interaction between the black hole and the material should have an effect on the black hole, too - as it gains material, it should also gain in mass.
Extreme Black Holes Appear to Have Wavy Hair Mysterious Universe - January 30, 2021

Extreme Kerr black holes have gravitational hair that can be measured at finite distances and violates the uniqueness theorems. This gravitational hair can in principle be detected by gravitational-wave detectors.
Black holes gain new powers when they spin fast enough PhysOrg - December 12, 2020
General relativity is a profoundly complex mathematical theory, but its description of black holes is amazingly simple. A stable black hole can be described by just three properties: its mass, its electric charge and its rotation or spin. Since black holes aren't likely to have much charge, it really takes just two properties. If you know a black hole's mass and spin, you know all there is to know about the black hole.
Earth faster, closer to black hole in new map of galaxy PhysOrg - November 27, 2020
Earth just got 7 km/s faster and about 2000 light-years closer to the supermassive black hole in the center of the Milky Way Galaxy. But don't worry, this doesn't mean that our planet is plunging towards the black hole. Instead the changes are results of a better model of the Milky Way Galaxy based on new observation data, including a catalog of objects observed over the course of more than 15 years by the Japanese radio astronomy project VERA.
Earth Is a Whole Lot Closer to Our Galaxy's Supermassive Black Hole Than We Thought Science Alert - November 27, 2020
According to a new map of the Milky Way galaxy, the Solar System's position isn't where we thought it was. Not only is it closer to the galactic centre - and the supermassive hole therein, Sagittarius A* - it's orbiting at a faster clip.
The black hole always chirps twice: Scientists find clues to decipher the shape of black holes PhysOrg - October 8, 2020
A team of gravitational wave researchers led by the ARC Center of Excellence for Gravitational Wave Discovery (OzGrav) report that when two black holes collide and merge, the remnant black hole "chirps" not once, but multiple times, emitting gravitational waves - intense ripples in the fabric space and time - that reveal information about its shape. Black holes are among the most fascinating objects in the universe. At their surface, known as the event horizon, gravity is so strong that not even light can escape. Usually, black holes are silent objects that swallow anything that falls too closely to them; however, when two black holes collide and merge, they produce one of the most catastrophic events in universe: In a fraction of a second, a highly deformed black hole forms and releases tremendous amounts of energy as it settles to its final state. This phenomenon gives astronomers a unique chance to observe rapidly changing black holes and explore gravity in its most extreme form.
Are some black holes wormholes in disguise? Gamma-ray blasts may shed clues Space.com -September 25, 2020

Unusual flashes of gamma rays could reveal that what appear to be giant black holes are actually huge wormholes, a new study finds. Wormholes are tunnels in space-time that can theoretically allow travel anywhere in space and time, or even into another universe. Einstein's theory of general relativity suggests wormholes are possible, although whether they really exist is another matter.
Gravitational waves point scientists to elusive missing-link black hole Space.com - September 2, 2020
Since 2015, astrophysicists have been using gravitational-wave detectors to "hear" chirp-like signals and decode massive collisions that send subtle ripples across spacetime. Now, scientists have heard a new kind of sound, a fast, deep "bang" that could unlock even more cosmic secrets, according to new research from the Laser Interferometer Gravitational-wave Observatory (LIGO) and its European counterpart, Virgo.
What happens if black holes fall into wormholes? A new way to find out. Space.com - August 11, 2020
Astronomers think they might be able to detect black holes falling into wormholes using ripples in spacetime known as gravitational waves, but only if wormholes actually exist and such a scenario ever happened, a new study finds. According to Einstein, who first predicted the existence of gravitational waves in 1916, gravity results from the way in which mass warps space and time. When two or more objects move within a gravitational field, they produce gravitational waves that travel at the speed of light, stretching and squeezing space-time along the way.
We Have Ploonets. We Have Moonmoons. Now Hold Onto Your Hats For... Blanets - Black Hole Planets Science Alert - August 4, 2020
It's easy to think of black holes as voracious destruction machines, slurping up everything in their immediate vicinity. But that's not always the case. The environments around active supermassive black holes are complex, and last year, a team of astronomers showed that there's a safe zone around each supermassive black hole in which thousands of planets could be orbiting. Now a team in Japan has given a new name to these black hole planets - "Blanets" which is just delightful - and worked out how these blanets might form from the grains of dust swirling around the black hole.
Thousands of Earthlike 'blanets' might circle the Milky Way's central black hole Live Science - August 4, 2020
Supermassive black holes dot our universe, monstrous gravity wells that bind galaxies together and wreath themselves in whirling cocoons of dust that emit bright X-ray beams. Sometimes, bright columns of matter burst up from their poles, forming jets visible across space. And now some scientists suspect these gravitational monsters might host blanets - tens of thousands of them. Scientists suggest calling these black hole planets by the name "blanets." Such blanets would form from the clouds of whirling dust that circle black holes. And they wouldn't be too different from planets that orbit normal stars. Some would be hard and rocky, like Earth, though likely as much as 10 times larger. Some would be gas giants, like our solar system's Neptune. They'd almost certainly be invisible to us, hidden in the disk of matter that birthed them and dwarfed by their supermassive parents.
For The First Time Ever, Astronomers Have Witnessed a Black Hole 'Blink' Science Alert - July 17, 2020

Black holes don't glow - in fact, they're famous for doing the opposite. But if they're actively devouring material from the space around them, that material can blaze like a billion X-ray Suns. And for the first time, astronomers have now seen that blaze mysteriously snuffed out, before gradually returning to brightness. The supermassive black hole is a beast clocking in at 19 million solar masses, powering a galactic nucleus 275 million light-years away, in a galaxy called 1ES 1927+654. Over a period of just 40 days, astronomers watched as its corona absolutely plummeted in brightness, before rising again to shine brighter than before.
Cases of black hole mistaken identity PhysOrg - July 15, 2020

Based on the current picture held by astronomers many black holes immersed in such a cocoon (referred to as "heavily obscured" black holes) should exist. However, this type of growing black hole is notoriously difficult to find, and until now the observed number has fallen short of predictions - even in the deepest images like the CDF-S.
About 10 million light-years from Earth, a blurry galaxy named Mirach's Ghost may help unravel a dark mystery: where the largest black holes in the universe came from Live Science - July 15, 2020
About 10 million light-years from Earth, a blurry galaxy named Mirach's Ghost (NGC 404) may help unravel a dark mystery: where the largest black holes in the universe came from. But this ghostly galaxy has also deepened the mystery surrounding these objects' births. A black hole is a singularity, a region in space-time where matter has gotten too dense to sustain itself, and collapsed into a formless point. Supermassive black holes (SMBHs) are cosmic monsters, often weighing billions of times the mass of our sun, as compared to the mass of heavy stars that form ordinary black holes. They sit at the centers of large galaxies, sucking up gas and whipping stars around with their immense gravities. There's one at the center of the Milky Way and an even larger one at the center of the Virgo A galaxy that astronomers have photographed. But it's still not clear how these mammoth objects formed.
Ellie, Antarctica, UFOs, Black Holes, Simulation Theory

Mysterious Particles Found in Antarctica Came From a Supermassive Black Hole Mysterious Universe - July 4, 2020

Remember the stories just a few months ago about NASA allegedly finding a parallel universe over Antarctica where time appears to run backwards? Those stories originated with a frustrating fact that has baffled scientists at a loss for an answer - what are the strange subatomic particles known as neutrinos doing in Antarctica and where did they come from? As we suspected in reporting that seemingly unbelievable story, it wasn’t from a reverse parallel universe. However, the real place it appears they may have originated from is just as unbelievable - a supermassive black hole.
A Behemoth Black Hole That Brings an End to Time and Space and the Laws of Physics Daily Galaxy - July 1, 2020

A gargantuan black hole, known as J2157, 34 billion times the mass of our sun mass, and about 8,000 times bigger than the black hole in the center of the Milky Way, gorges on nearly the equivalent of one sun every day about a monster of the early universe that brings an end to time and space and the laws of physics.
This Absolute Monster of a Black Hole Eats The Equivalent of a Sun a Day Science Alert - July 2, 2020
One of the largest known black holes in the Universe has turned out to have an appetite to match its prodigious size. New measurements reveal that it's an absolute chonk, clocking in at around 34 billion times the mass of the Sun - and it devours almost one Sun's worth of mass every day.This makes it the fastest-growing black hole we know of in the entire Universe; its enormity tips it into the category of ultramassive black holes.
For The First Time Ever, Astronomers Detect Light From a Black Hole Collision Science Alert - June 26, 2020
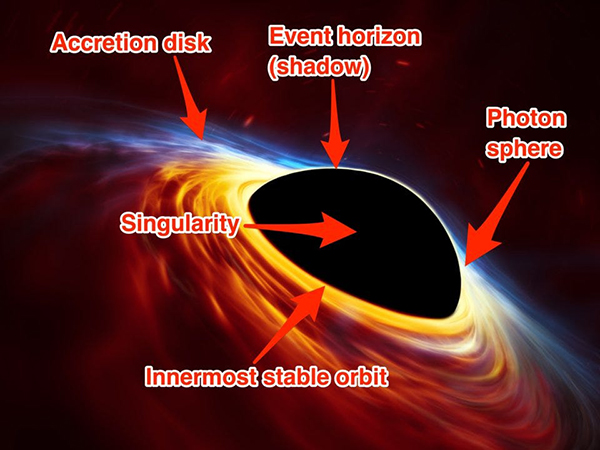
For the first time, astronomers have seen a flash of light from the collision of two black holes. The objects met and merged 7.5 billion light-years away, within a vortex of hot, swirling matter circling a larger, supermassive black hole. This whirlpool is called the accretion disk, and it orbits a black hole's event horizon – the point after which gravity is so powerful that not even light can escape. That's why scientists have never seen two black holes collide. In the absence of light, they can only identify such mergers by detecting their gravitational waves – ripples in spacetime created by the collisions of massive objects.
Monster black hole found in the early universe Science Alert - June 25, 2020
Astronomers have discovered the second-most distant quasar ever found using three Maunakea Observatories in Hawai'i: W. M. Keck Observatory, the international Gemini Observatory, a Program of NSF's NOIRLab, and the University of Hawai'i-owned United Kingdom Infrared Telescope (UKIRT). It is the first quasar to receive an indigenous Hawaiian name, Poniua'ena, which means "unseen spinning source of creation, surrounded with brilliance" in the Hawaiian language.
Black hole's heart still beating PhysOrg - June 10, 2020
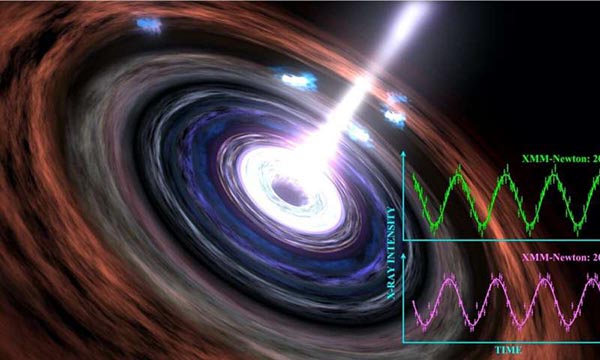
The first confirmed heartbeat of a supermassive black hole is still going strong more than ten years after first being observed.
Astronomers discover closest black hole to Earth. And you can 'see' it. Live Science - May 6, 2020

A newfound black hole may be the closest black hole to Earth, and you can spot its cosmic home in the night sky without a telescope.
The black hole, which is lurking 1,000 light-years from Earth in the southern constellation of Telescopium, belongs to a system with two companion stars that are bright enough to observe with the naked eye. But you won't be able to see the black hole itself; the massive object has such a strong gravitational pull that nothing - not even light - can escape it.
Video: 'Nearest black hole to Earth discovered' BBC - May 6, 2020

Astronomers have a new candidate in their search for the nearest black hole to Earth. It's about 1,000 light-years away, or roughly 9.5 thousand, million, million km, in the Constellation Telescopium. That might not sound very close, but on the scale of the Universe, it's actually right next door. Scientists discovered the black hole from the way it interacts with two stars - one that orbits the hole, and the other that orbits this inner pair. Normally, black holes are discovered from the way they interact violently with an accreting disc of gas and dust. As they shred this material, copious X-rays are emitted. It's this high-energy signal that telescopes detect, not the black hole itself.
So this is an unusual case, in that it's the motions of the stars, together known as HR 6819, that have given the game away.
Astronomers have discovered a black hole lying just 1,000 light-years from Earth. Science Daily - May 6, 2020

A team of astronomers from the European Southern Observatory (ESO) and other institutes has discovered a black hole lying just 1000 light-years from Earth. The black hole is closer to our Solar System than any other found to date and forms part of a triple system that can be seen with the naked eye. The team found evidence for the invisible object by tracking its two companion stars using the MPG/ESO 2.2-metre telescope at ESO's La Silla Observatory in Chile. They say this system could just be the tip of the iceberg, as many more similar black holes could be found in the future.
Very Large Telescope sees star dance around supermassive black hole, proves Einstein right PhysOrg - April 16, 2020

Observations made with ESO's Very Large Telescope (VLT) have revealed for the first time that a star orbiting the supermassive black hole at the centre of the Milky Way moves just as predicted by Einstein's general theory of relativity. Its orbit is shaped like a rosette and not like an ellipse as predicted by Newton's theory of gravity. This long-sought-after result was made possible by increasingly precise measurements over nearly 30 years, which have enabled scientists to unlock the mysteries of the behemoth lurking at the heart of our galaxy.
Hologram Within a Hologram Hints at Fate of Black Holes Quanta Magazine - December 5, 2019

Like cosmic hard drives, black holes pack troves of data into compact spaces. But ever since Stephen Hawking calculated in 1974 that these dense spheres of extreme gravity give off heat and fade away, the fate of their stored information has haunted physicists. The problem is this: The laws of quantum mechanics insist that information about the past is never lost, including the record of whatever fell into a black hole. But Hawking's calculation contradicted this. He applied both quantum mechanics and Albert Einstein's theory of gravity to the space around a black hole and found that quantum jitters cause the black hole to emit radiation that’s perfectly random, carrying no information. As this happens the black hole shrinks and eventually disappears.
This ultra-massive black hole just broke a record - The study refers to this process as positive feedback - A black hole is creating stars rather than stopping their production or consuming them

Much like stars and planets, black holes also fall into different categories. Astronomers have now spotted a record-breaking heavyweight black hole at the center of a galaxy known as Holm 15A. The black hole weighs 40 billion times the mass of our sun.
Mysterious Supermassive Black Hole is Creating Stars Across Four Galaxies- Story 2
First 'overtones' heard in the ringing of a black hole PhysOrg - September 12, 2019
When two black holes collide, they merge into one bigger black hole and ring like a struck bell, sending out ripples in space and time called gravitational waves. Embedded in these gravitational waves are specific frequencies, or tones, which are akin to individual notes in a musical chord.
A Distant Black Hole Brightens Every 9 Hours, and No One Knows Why Live Science - September 12, 2019
A black hole at the center of a distant galaxy is behaving like no other black hole astronomers have ever seen. Every 9 hours, the black hole at the center of galaxy GSN 069, about 250 million light years away, sends a bright stream of X-rays toward Earth. It's an active black hole, so it's always gobbling up matter; in the process, that matter heats up and emits some light as it falls toward the event horizon around the singularity, the point beyond which no light or matter can escape. But in 2018, researchers who were using the European Space Agency's (ESA) XMM-Newton telescope realized that, at every peak of that 9-hour cycle, the GSN 069 black hole would get about 100 times brighter on the X-ray spectrum.
The Largest Black Holes in the Universe Formed in a Snap - Then Stopped Live Science - July 5, 2019
About 13 billion years ago, when our universe was still just a scrappy startup, the cosmos hit a creative streak and churned out supermassive black holes left, right and center. Astronomers can still sneak a peek at these relics of the early universe when they look at quasars, incredibly large, outstandingly bright objects thought to be powered by old black holes billions of times more massive than Earth's sun. However, the very existence of these ancient objects poses a problem. Many quasars appear to originate from the first 800 million years of the universe, long before any stars could grow big or old enough to collapse under their own mass, explode in a supernova and form a black hole. So, where are these old holes in the fabric of space-time coming from? According to one popular theory, maybe all it takes is a whole lot of gas
Most-detailed-ever simulations of black hole solve longstanding mystery PhysOrg - June 6, 2019
An international team has constructed the most detailed, highest resolution simulation of a black hole to date. The simulation proves theoretical predictions about the nature of accretion disks—the matter that orbits and eventually falls into a black hole - that have never before been seen.
Scientists have finally revealed the first ever images of a black hole's event horizon in groundbreaking feat. Researchers with Event Horizon Telescope used eight radio observatories around the world to collect data Scientists were able to capture silhouette of a black hole, revealing its shape based on glowing ring around it. Using a virtual telescope built from eight radio observatories positioned at different points on the globe, the international team has spent the last few years probing Sagittarius A*, the supermassive black hole at the heart of the Milky Way, and another target called M87 in the Virgo cluster of galaxies. While black holes are invisible by nature, the ultra-hot material swirling in their midst forms a ring of light around the perimeter that reveals the mouth of the object itself based on its silhouette. This boundary is known as the event horizon.
All Your Questions About the New Black Hole Image Answered Live Science - April 11, 2019

Video: The stunning black hole photo: What you're seeing CNN - April 10, 2019

First ever black hole image released BBC - April 10, 2019

Working together as a 'virtual telescope,' observatories around the world produce first direct images of a black hole Science Daily - April 10, 2019
Seeing the unseeable: Scientists unveil the first ever direct image of a black hole captured by global 'virtual telescope' Daily Mail - April 10, 2019
Amazing simulation gives you a virtual tour of the violent black hole at the centre of our galaxy Daily Mail - November 19, 2018
n amazing simulation gives you a virtual tour of the violent black hole at the centre of the Milky Way galaxy. The animation shows dust and gas whipping around the edges of Sagittarius A* at speeds of up to 56,000 miles per second (90,000 kilometres per second). Scientists know the supermassive black hole sits in the middle of our galaxy, but have yet to get a good look at it because it is hidden behind huge plumes of gas.
Researchers reveal the story of the oldest stars and galaxies, compiled from 20 years of simulating the early universe PhysOrg - October 17, 2018
 BR>
The Big Bang has captured our imagination like no other theory in science: the magnificent, explosive birth of our Universe. But do you know what came next? Code was created which allowed formation of the first stars in the universe to be modeled. These equations describe the movement and chemical reactions inside gas clouds in a universe before light, and the immense gravitational pull of a much larger but invisible mass of mysterious dark matter.
BR>
The Big Bang has captured our imagination like no other theory in science: the magnificent, explosive birth of our Universe. But do you know what came next? Code was created which allowed formation of the first stars in the universe to be modeled. These equations describe the movement and chemical reactions inside gas clouds in a universe before light, and the immense gravitational pull of a much larger but invisible mass of mysterious dark matter.
Magnetic fields may be the key to black hole activity PhysOrg - October 17, 2018
SOFIA data indicate that magnetic fields are trapping and confining dust near the center of the active galaxy, Cygnus A, and feeding material onto the supermassive black hole at its center. The unified model, which attempts to explain the different properties of active galaxies, states that the core is surrounded by a donut-shaped dust cloud, called a torus. How this obscuring structure is created and sustained has never been clear, but these new results from SOFIA indicate that magnetic fields may be responsible for keeping the dust close enough to be devoured by the hungry black hole. In fact, one of the fundamental differences between active galaxies like Cygnus A and their less active cousins, like our own Milky Way, may be the presence or absence of a strong magnetic field around the black hole.
Simulation Shows How Monster Black Holes Glow Before They Collide Space.com - October 4, 2018
A new model suggests that merging supermassive black holes will glow in eerie ultraviolet and X-ray light as they spiral into an inevitable crash. Supermassive black holes are millions or billions of times the mass of the sun and reside in just about every galaxy that is at least the size of our own Milky Way, according to a NASA statement. Scientists know that galaxies commonly combine; this will happen with the Milky Way and Andromeda, for example, in about 4 billion years.
Have scientists found evidence of another Universe? 'Ghost black hole' from ancient universe that died before the Big Bang has been discovered, physicists claim Daily Mail - August 25, 2018

Scientists have found that the universe we live in is not the first one to ever exist. A group of leading physicists have found that eons ago, other universes existed and they had black holes, just like the current universe. They say that cosmic microwave background radiation (CMB) - the same thing that causes white noise on TVs - is evidence of the remnants of these blackholes. These leading thinkers are now calling for a modified version of the Big Bang to account for this multiverse theory. The theory is called conformal cyclic cosmology, or CCC, and states that universes develop, expand and die in sequence. The black holes in each one then leaves its mark on the following universe that follow.
Holographic image of a black hole proposed in a graphene flake PhysOrg - July 30, 2018
The type of holographic duality illustrated by the SYK model is particularly interesting because it exhibits some of the signature properties of black holes, such as non-zero residual entropy and quantum chaos propagation. It may also help answer fundamental questions about the connection between quantum mechanics and gravity.
Black hole hologram appears in a graphene flake Physics World - July 30, 2018
Astronomers find fastest-growing black hole known in space describing it as a monster that devours a mass equivalent to our sun every two days PhysOrg - May 15, 2018
The astronomers have looked back more than 12 billion years to the early dark ages of the Universe, when this supermassive black hole was estimated to be the size of about 20 billion suns with a one per cent growth rate every one million years.
Is Dark Matter Made Up of Mini Black Holes from the Big Bang? Live Science - April 6, 2018
Dark matter, the mysterious extra mass in the universe that emits no light yet exerts a gravitational pull, may actually be made up of primordial black holes that originated with the Big Bang. And these mini black holes can thank the Higgs boson for their birth - at least according to a new theory. This theory posits that these primeval black holes were created from instabilities in the field that gives rise to the Higgs Boson, the mysterious "God" particle discovered at the Large Hadron Collider (LHC).
Dozen black holes found at galactic centre BBC - April 5, 2018
A dozen black holes may lie at the centre of our galaxy, the Milky Way, researchers have said. A new analysis provides support for a decades-old prediction that "supermassive" black holes at the centers of galaxies are surrounded by many smaller ones. However, previous searches of the Milky Way's centre, where the nearest supermassive black hole is located, have found little evidence for this. In addition, black holes from outside the halo are believed to fall under the influence of Sgr A* as they lose their energy, causing them to be pulled into its vicinity, where they are held captive by its force. Some of these bind - or "mate" - to passing stars, forming binary systems. Previous attempts to detect this population of black holes have looked for the bright bursts of X-rays that are sometimes emitted by black hole binaries.
Astronomers Spy Swarms of Black Holes at Our Galaxy's Core Scientific American - April 4, 2018
For the first time astronomers have glimpsed a long-predicted population of black holes lurking at the heart of the Milky Way.
Scientists already knew our galaxy’s core holds a supermassive black hole weighing millions of times more than our sun, and that this great beast is enveloped by a diverse entourage of lesser companions. Trapped in its gravitational clutches, run-of-the-mill stars whip around this gargantuan black hole like fireflies in a hurricane. So, too, do astrophysical exotica such as neutron stars and white dwarfs - the remnants left by normal stars when they die. Presumably black holes should be there as well, either born on the galactic center’s doorstep from the deaths of massive stars or arriving via migration from farther out.
Black holes might be portals to alternate universes Syfy - February 27, 2018
Black holes are called “black holes” for a reason. No one knows what lies beyond that impenetrable darkness, and there is no spacecraft in existence (and obviously no human) that could possibly make it past an event horizon and withstand the crushing gravity. But are there exceptions?
Some black holes erase your past Science Daily - February 22, 2018
Physicists insist on determinism: your past and present determine your future uniquely, per Einstein's equations of general relativity. They call this strong cosmic censorship. A mathematician found some types of black holes -- charged, non-rotating objects in an expanding universe -- that allow an observer inside the black hole to travel across a horizon into a place where the past is obliterated and there are an infinite number of possible futures for every initial state.
The concept of a body so massive that not even light could escape from it was put forward by the English geologist John Michell in a 1783 paper sent to the Royal Society. At that time, the Newtonian theory of gravity and the concept of escape velocity were well known. Michell computed that a body 500 times the radius of the Sun and of the same density would have at its surface an escape velocity equal to the speed of light, and therefore would be invisible. Although he thought it unlikely, Michell considered the possibility that many such objects that cannot be seen might be present in the cosmos.
In 1796, the French mathematician Pierre-Simon Laplace promoted the same idea in the first and second edition of his book Exposition du Systeme du Monde. It disappeared in later editions. The whole idea gained little attention in the 19th century, since light was thought to be a massless wave, not influenced by gravity.
In 1915, Albert Einstein developed his theory of general relativity, having earlier shown that gravity does influence light's motion. Only a few months later, Karl Schwarzschild found a solution to the Einstein field equations, which describes the gravitational field of a point mass and a spherical mass.[8] A few months after Schwarzschild, Johannes Droste, a student of Hendrik Lorentz, independently gave the same solution for the point mass and wrote more extensively about its properties. This solution had a peculiar behavior at what is now called the Schwarzschild radius, where it became singular, meaning that some of the terms in the Einstein equations became infinite. The nature of this surface was not quite understood at the time.
In 1924, Arthur Eddington showed that the singularity disappeared after a change of coordinates (see Eddington–Finkelstein coordinates), although it took until 1933 for Georges LemaĒtre to realize that this meant the singularity at the Schwarzschild radius was an unphysical coordinate singularity.
In 1931, Subrahmanyan Chandrasekhar calculated, using special relativity, that a non-rotating body of electron-degenerate matter above a certain limiting mass (now called the Chandrasekhar limit at 1.4 solar masses) has no stable solutions. His arguments were opposed by many of his contemporaries like Eddington and Lev Landau, who argued that some yet unknown mechanism would stop the collapse. They were partly correct: a white dwarf slightly more massive than the Chandrasekhar limit will collapse into a neutron star, which is itself stable because of the Pauli exclusion principle.
But in 1939, Robert Oppenheimer and others predicted that neutron stars above approximately three solar masses (the Tolman–Oppenheimer–Volkoff limit) would collapse into black holes for the reasons presented by Chandrasekhar, and concluded that no law of physics was likely to intervene and stop at least some stars from collapsing to black holes. Oppenheimer and his co-authors interpreted the singularity at the boundary of the Schwarzschild radius as indicating that this was the boundary of a bubble in which time stopped. This is a valid point of view for external observers, but not for infalling observers. Because of this property, the collapsed stars were called "frozen stars", because an outside observer would see the surface of the star frozen in time at the instant where its collapse takes it inside the Schwarzschild radius. p the collapse. His arguments were opposed by Arthur Eddington, who believed that something would inevitably stop the collapse.
In 1958, David Finkelstein identified the Schwarzschild surface as an event horizon, "a perfect unidirectional membrane: causal influences can cross it in only one direction". This did not strictly contradict Oppenheimer's results, but extended them to include the point of view of infalling observers. Finkelstein's solution extended the Schwarzschild solution for the future of observers falling into a black hole. A complete extension had already been found by Martin Kruskal, who was urged to publish it.
In 1963, Roy Kerr found the exact solution for a rotating black hole. Two years later, Ezra Newman found the axisymmetric solution for a black hole that is both rotating and electrically charged. Through the work of Werner Israel, Brandon Carter, and David Robinson the no-hair theorem emerged, stating that a stationary black hole solution is completely described by the three parameters of the Kerr-Newman metric; mass, angular momentum, and electric charge.
These results came at the beginning of the golden age of general relativity, which was marked by general relativity and black holes becoming mainstream subjects of research. This process was helped by the discovery of pulsars in 1967, which, by 1969, were shown to be rapidly rotating neutron stars. Until that time, neutron stars, like black holes, were regarded as just theoretical curiosities; but the discovery of pulsars showed their physical relevance and spurred a further interest in all types of compact objects that might be formed by gravitational collapse.
At first, it was suspected that the strange features of the black hole solutions were pathological artifacts from the symmetry conditions imposed, and that the singularities would not appear in generic situations. This view was held in particular by Vladimir Belinsky, Isaak Khalatnikov, and Evgeny Lifshitz, who tried to prove that no singularities appear in generic solutions. However, in the late 1960s Roger Penrose and Stephen Hawking used global techniques to prove that singularities appear generically.
The first use of the term "black hole" in print was by journalist Ann Ewing in her article "'Black Holes' in Space", dated 18 January 1964, which was a report on a meeting of the American Association for the Advancement of Science.
John Wheeler used term "black hole" a lecture in 1967, leading some to credit him with coining the phrase. After Wheeler's use of the term, it was quickly adopted in general use.
Work by James Bardeen, Jacob Bekenstein, Carter, and Hawking in the early 1970s led to the formulation of black hole thermodynamics. These laws describe the behavior of a black hole in close analogy to the laws of thermodynamics by relating mass to energy, area to entropy, and surface gravity to temperature.
The analogy was completed when Hawking, in 1974, showed that quantum field theory predicts that black holes should radiate like a black body with a temperature proportional to the surface gravity of the black hole.
No Black Holes Exist, Says Stephen Hawking - At Least Not Like We Think - National Geographic - January 27, 2014
Black holes do not exist - at least, not as we know them, says renowned physicist Stephen Hawking, potentially provoking a rethink of one of space's most mysterious objects. A new study from Hawking also says that black holes may not possess "firewalls," destructive belts of radiation that some researchers have proposed would incinerate anything that passes through them but others scientists deem an impossibility. The conventional view of black holes posits that their gravitational pull is so powerful that nothing can escape from them - not even light, which is why they're called black holes. The boundary past which there is supposedly no return is known as the event horizon. In this conception, all information about anything that ventures past a black hole's event horizon is destroyed. On the other hand, quantum physics, the best description so far of how the universe behaves on a subatomic level, suggests that information cannot ever be destroyed, leading to a fundamental conflict in theory. Now Hawking is suggesting a resolution to the paradox: Black holes do not possess event horizons after all, so they do not destroy information.
The defining feature of a black hole is the appearance of an event horizon - a boundary in spacetime through which matter and light can only pass inward towards the mass of the black hole. Nothing, not even light, can escape from inside the event horizon. The event horizon is referred to as such because if an event occurs within the boundary, information from that event cannot reach an outside observer, making it impossible to determine if such an event occurred.
As predicted by general relativity, the presence of a mass deforms spacetime in such a way that the paths taken by particles bend towards the mass. At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.
To a distant observer, clocks near a black hole appear to tick more slowly than those further away from the black hole. Due to this effect, known as gravitational time dilation, an object falling into a black hole appears to slow down as it approaches the event horizon, taking an infinite time to reach it.
At the same time, all processes on this object slow down, for a fixed outside observer, causing emitted light to appear redder and dimmer, an effect known as gravitational redshift.[49] Eventually, at a point just before it reaches the event horizon, the falling object becomes so dim that it can no longer be seen.
On the other hand, an observer falling into a black hole does not notice any of these effects as he crosses the event horizon. According to his own clock, he crosses the event horizon after a finite time without noting any singular behavior. In particular, he is unable to determine exactly when he crosses it, as it is impossible to determine the location of the event horizon from local observations.
The shape of the event horizon of a black hole is always approximately spherical. For non-rotating (static) black holes the geometry is precisely spherical, while for rotating black holes the sphere is somewhat oblate.
Black hole hums B flat BBC - September 10, 2003
Astronomers have detected sound waves from a super-massive black hole. The "note" is the deepest ever detected from an object in the Universe. The black hole lives in the Perseus cluster of galaxies, located 250 million light-years away. The tremendous amounts of energy carried from the black hole by these sound waves may solve a longstanding problem in astrophysics. The pitch of the sound can be determined. Although far too low to be heard, it is calculated to be B flat.
At the center of the black hole, well inside the event horizon, general relativity predicts a singularity, a place where the curvature of space-time becomes infinite and gravitational forces become infinitely strong. Space-time inside the event horizon is peculiar in that the singularity is in every observer's future, so all particles within the event horizon move inexorably towards it. This means that there is a conceptual inaccuracy in the non-relativistic concept of a black hole as originally proposed by John Michell in 1783.
It is expected that future refinements or generalizations of general relativity (in particular quantum gravity) will change what is thought about the nature of black hole interiors. Most theorists interpret the mathematical singularity of the equations as indicating that the current theory is not complete, and that new phenomena must come into play as one approaches the singularity. The question may be largely academic, as the cosmic censorship hypothesis asserts that there are no naked singularities in general relativity: Every singularity is hidden behind an event horizon and cannot be probed.
Another school of thought holds that no singularity occurs, because of a bubble-like local inflation in the interior of the collapsing star. Radii stop converging as they approach the event horizon, are parallel at the horizon, and begin diverging in the interior. The solution resembles a wormhole (from the exterior to the interior) in a neighborhood of the horizon, with the horizon as the neck.
In Michell's theory, the escape velocity equals the speed of light, but it would still, for example, be theoretically possible to hoist an object out of a black hole using a rope. General relativity eliminates such loopholes, because once an object is inside the event horizon, its time-line contains an end-point to time itself, and no possible world-lines come back out through the event horizon.
According to theory, the event horizon of a black hole that is not spinning is spherical, and its singularity is (informally speaking) a single point. If the black hole carries angular momentum (inherited from a star that is spinning at the time of its collapse), it begins to drag space-time surrounding the event horizon in an effect known as frame-dragging.
This spinning area surrounding the event horizon is called the ergosphere and has an ellipsoidal shape. Since the ergosphere is located outside the event horizon, objects can exist within the ergosphere without falling into the hole. However, because space-time itself is moving in the ergosphere, it is impossible for objects to remain in a fixed position. Objects grazing the ergosphere could in some circumstances be catapulted outwards at great speed, extracting energy (and angular momentum) from the hole, hence the name ergosphere ("sphere of work") because it is capable of doing work.
The effects of a black hole's gravity as described by the Theory of Relativity cause a number of peculiar effects. An object approaching simple Schwarzschild-type (non-rotating) black hole's center will appear to distant observers as having an increasingly slow descent as the object approaches the event horizon. This is because a photon takes an increasingly long time to escape from the pull of the black hole to allow the distant observer to gain information on the object's fate.
From the object's frame of reference, it will cross the event horizon and reach the singularity, or center of the black hole, all within a finite amount of time. Once the object crosses over the event horizon, light will no longer escape the black hole, and the object can no longer be observed outside of the black hole. As the object continues to approach the singularity, it will elongate, and the parts closest to the singularity will begin to red shift, until they finally become invisible. Nearing the singularity, the gradient of the gravitational field from head to foot will become considerable, will stretch and tear because of tidal forces: the parts closest to the singularity feel disproportionately stronger gravitational force than those parts farther away. This process is known as spaghetti-fication.
In 1971, Stephen Hawking showed that the total area of the event horizons of any collection of classical black holes can never decrease. This sounded remarkably similar to the Second Law of Thermodynamics, with area playing the role of entropy. Classically, one could violate the second law of thermodynamics by material entering a black hole disappearing from our universe and resulting in a decrease of the total entropy of the universe.
Therefore, Jacob Bekenstein proposed that a black hole should have an entropy and that it should be proportional to its horizon area. Since black holes do not classically emit radiation, the thermodynamic viewpoint was simply an analogy. However, in 1974, Hawking applied quantum field theory to the curved space-time around the event horizon and discovered that black holes can emit thermal radiation, known as Hawking radiation.
Using the first law of black hole mechanics, it follows that the entropy of a black hole is one quarter of the area of the horizon. This is a universal result and can be extended to apply to cosmological horizons such as in de Sitter spacetime. It was later suggested that black holes are maximum-entropy objects, meaning that the maximum entropy of a region of space is the entropy of the largest black hole that can fit into it. This led to the holographic principle.
Hawking radiation originates just outside the event horizon and, so far as it is understood, does not carry information from its interior since it is thermal. However, this means that black holes are not completely black: the effect implies that the mass of a black hole slowly evaporates with time. Although these effects are negligible for astronomical black holes, they are significant for hypothetical very small black holes where quantum-mechanical effects dominate. Indeed, small black holes are predicted to undergo runaway evaporation and eventually vanish in a burst of radiation. Hence, every black hole that cannot consume new mass has a finite life that is directly related to its mass.
On 21 July 2004 Stephen Hawking presented a new argument that black holes do eventually emit information about what they swallow, reversing his previous position on information loss. He proposed that quantum perturbations of the event horizon could allow information to escape from a black hole, where it can influence subsequent Hawking radiation . The theory has not yet been reviewed by the scientific community and if it is accepted it is likely to resolve the black hole information paradox. In the meantime, the announcement has attracted a lot of attention in the media.
Formation
General relativity (as well as most other metric theories of gravity) not only says that black holes can exist, but in fact predicts that they will be formed in nature whenever a sufficient amount of mass gets packed in a given region of space, through a process called gravitational collapse. As the mass inside that region increases, its gravity becomes stronger - or, in the language of relativity, the space around it becomes increasingly deformed. When the escape velocity at a certain distance from the center reaches the speed of light, an event horizon is formed within which matter must inevitably collapse onto a single point, forming a singularity.
A quantitative analysis of this idea led to the prediction that a star remaining about three times the mass of the Sun at the end of its evolution (usually as a neutron star), will almost inevitably shrink to the critical size needed to undergo a gravitational collapse. Once it starts, the collapse cannot be stopped by any physical force, and a black hole is created.
Stellar collapse will generate black holes containing at least three solar masses. Black holes smaller than this limit can only be created if their matter is subjected to sufficient pressure from some source other than self-gravitation. The enormous pressures needed for this are thought to have existed in the very early stages of the universe, possibly creating primordial black holes which could have masses smaller than that of the Sun.
Supermassive black holes containing millions to billions of solar masses could also form wherever a large number of stars are packed in a relatively small region of space, or by large amounts of mass falling into a "seed" black hole, or by repeated fusion of smaller black holes. The necessary conditions are believed to exist in the centers of some (if not most) galaxies, including our own Milky Way .
Theory says that we cannot detect black holes by light that is emitted or reflected by the matter inside them. However, those objects can be inductively detected from observation of phenomena near them, such as gravitational lensing and stars that appear to be in orbit around space where there is no visible matter.
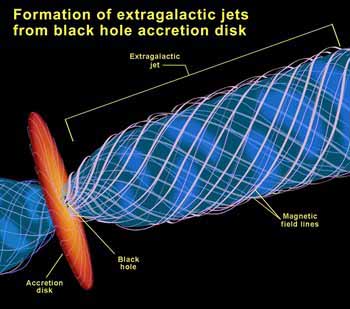
The most conspicuous effects are believed to come from matter falling into a black hole, which (like water flowing into a drain) is predicted to collect into an extremely hot and fast-spinning accretion disk around the object before being swallowed by it. Friction between adjacent zones of the disk causes it to become extremely hot and emit large amounts of X-rays. This heating is extremely efficient and can convert about 50% of the mass energy of an object into radiation, as opposed to nuclear fusion which can only convert a few percent of the mass to energy. Other predicted effects are narrow jets of particles at relativistic speeds squirting off along the disk's axis.
However, accretion disks, jets, and orbiting objects are found not only around black holes, but also around other objects such as neutron stars; and the dynamics of bodies near these non-black hole attractors is largely similar to the dynamics of bodies around black holes, and is currently a very complex and active field of research involving magnetic fields and plasma physics.
Hence, for the most part, observations of accretion disks and orbital motions merely indicate that there is a compact object of a certain mass, and says very little about 'the nature of that object. The identification of an object as a black hole requires the further assumption that no other object (or bound system of objects) could be so massive and compact. Most astrophysicists accept that this is the case, since according to general relativity, any concentration of matter of sufficient density must necessarily collapse into a black hole.
One important observable difference between black holes and other compact massive objects is that any in falling matter will eventually collide with the latter, at relativistic speeds, leading to irregular intense flares of X-rays and other hard radiation. Thus the lack of such flare-ups around a compact concentration of mass is taken as evidence that the object is a black hole, with no surface onto which matter can be suddenly dumped.
The formation of micro black holes on Earth in particle accelerators have been tentatively reported, but not yet confirmed. So far there are no observed candidates for primordial black holes. Read more ...