A fractal is a natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. If the replication is exactly the same at every scale, it is called a self-similar pattern. An example of this is the Menger Sponge. Fractals can also be nearly the same at different levels. Fractals also includes the idea of a detailed pattern that repeats itself. Read more ...
A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems - the pictures of Chaos. Geometrically, they exist in between our familiar dimensions. Fractal patterns are extremely familiar, since nature is full of fractals. For instance: trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc. Abstract fractals - such as the Mandelbrot Set - can be generated by a computer calculating a simple equation over and over.
A New Type of Fractal Has Been Discovered in Magnetic Ice Science Alert - December 20, 2022
Fractal patterns can be found everywhere from snowflakes to lightning to the jagged edges of coastlines. Beautiful to behold, their repetitive nature can also inspire mathematical insights into the chaos of the physical landscape. A new example of these mathematical oddities has been uncovered in a type of magnetic substance known as spin ice, and it could help us better understand how a quirky behavior called a magnetic monopole emerges from its unsettled structure. Spin ices are magnetic crystals that obey similar structural rules to water ices, with unique interactions governed by the spins of their electrons rather than the push and pull of charges. As a result of this activity, they don't have any one single low-energy state of minimal activity. Instead, they almost hum with noise, even at insanely low temperatures.
Is the Universe a Fractal? Universe Today - July 16, 2021
We find examples of fractals everywhere in nature. Tree branches, snowflakes, river deltas, cloud formations, and more. So it's natural to ask the ultimate question: is the entire universe one giant fractal? The answer isÉno, but sorta yes.
Scientists discover fractal patterns in a quantum material PhysOrg - October 18, 2019
A fractal is any geometric pattern that occurs again and again, at different sizes and scales, within the same object. This "self-similarity" can be seen throughout nature, for example in a snowflake's edge, a river network, the splitting veins in a fern, and the crackling forks of lightning. Now physicists at MIT and elsewhere have for the first time discovered fractal-like patterns in a quantum material - a material that exhibits strange electronic or magnetic behavior, as a result of quantum, atomic-scale effects.
Fractal edges shown to be key to imagery seen in Rorschach inkblots Science Daily - February 14, 2017

Researchers have unlocked the mystery of why people have seen so many different images in Rorschach inkblots. The image associations are induced by fractal characteristics at the edges of the blots and depend on the scaling parameters of the patterns, says researcher. Fractals are objects with irregular curves or shapes and are recognizable building blocks of nature. Trees, clouds, rivers, galaxies, lungs and neurons are fractals. The new discovery isn't about improving inkblots for psychological assessments -- their use became controversial and mostly set aside in the last 20 years. It does, however, have implications for Taylor's efforts to design a fractal based retinal implant and for potentially improving materials used for camouflage.
Researchers find evidence of fractal behavior in pulsating stars PhysOrg - February 4, 2015
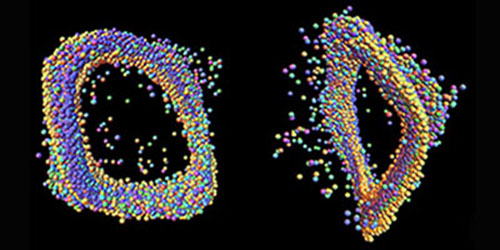
A team of researchers working at the University of Hawaii using data from the Kepler space telescope, has found that the oscillations made by a star conform closely to the golden mean further study showed that it also behaves in a fractal pattern. In studying the Kepler data, the team was able to track the pulses that emanated from the star over a period of four years taken at 30 minute intervals. They found that two of star KIC 5520878's pulsating frequencies occurred at 4.05 and a 6.41 hour cycles - which the team noted had a ratio of 1.58, which is close to 1.618, aka the Golden Ratio -famously found in nature and sometimes artistic renderings. Intrigued, they looked deeper and found that the frequencies conformed to fractal patterns separating the oscillations into their constituent parts revealed additional weaker frequencies, similar to the way, the team points out, that images of shorelines display craggy lines regardless of how close or far away they are viewed from.

Fractal Landscapes Created in Snow by Simon Beck - December 2013

Fractal patterns of early life revealed -- New Scientist - July 15, 2004

Newly uncovered fossils reveal in extraordinary clarity the strangeness of the Earth's earliest complex life. The finds show that the organisms were assembled in fractal patterns from frond-like building blocks. They were unable to move and had no reproductive organs, perhaps reproducing by dropping off new fronds. The creatures, which were neither animals or plants, are called "rangeomorphs". They first appeared on the ocean floor 575 million years ago, after the last global glaciation, and were among the first of the soft-bodied creatures in the Ediacaran period. This biota survived until 542 million years ago, when modern animals diversified rapidly in the Cambrian explosion and most Ediacaran species vanished.
Until now, almost all Ediacaran fossils were squashed flat, and the few that were not were poorly preserved. This led to debate over whether the poor preservation obscured links to later life, or if the Ediacaran organisms were in fact a failed experiment in evolution that simply became extinct. The newly unearthed fossils, from Newfoundland, Canada, were preserved three-dimensionally in fine-grained mud by a "one-in-a-million" streak of luck, says Guy Narbonne of Queen's University in Kingston, Ontario.
Just after a mud flow entombed the organisms, a nearby volcano erupted, covering it with a thick ash protective ash deposit. Later, the bed escaped the strain that altered most of the rock in the region. Now weathering is exposing them so "they basically pop out of the rock," Narbonne told New Scientist. "You are seeing what they looked like when they were alive." That exceptional preservation is cracking the mystery of Ediacara. In some spots the surface has eroded and "we see for the first time what was inside an Ediacaran fossil," Narbonne says. Each frond element, a few centimetres long, was made of many tubes held up by a semi-rigid organic skeleton.
The frond elements had branches which themselves had branches, a classic fractal structure. Frondlets assembled themselves like building blocks to make larger living structures attached to the sea floor. Narbonne found rangeomorphs assembled in several different shapes, which he believes filtered food from different levels of the water column, as well as isolated free-living frondlets.
The fractal patterns look complex, but Narbonne says their self-similarity means that very simple genomes - expected in early organisms - would suffice both to assemble individual frondlets and to control their assembly into larger structures. That would explain why the rangeomorphs evolved first. They accounted for over 80% of fossils early in the Ediacara period, when there were no mobile animals or traces of burrows. But they declined as more mobile animals evolved, apparently unable to compete, or perhaps being eaten themselves.
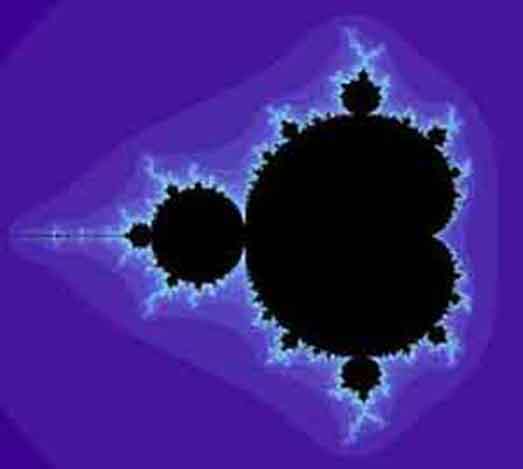
The Mandelbrot Set
When computed and graphed on the complex plane, the Mandelbrot Set is seen to have an elaborate boundary, which does not simplify at any given magnification. This qualifies the boundary as a fractal. The Mandelbrot set has become popular outside mathematics both for its aesthetic appeal and for being a complicated structure arising from a simple definition. Benoit Mandelbrot and others worked hard to communicate this area of mathematics to the public.

'Fractal' mathematician Benoit Mandelbrot dies aged 85
BBC - October 18, 2010
Benoit Mandelbrot, who discovered mathematical shapes known as fractals, has died of cancer at the age of 85. Mandelbrot, who had joint French and US nationality, developed fractals as a mathematical way of understanding the infinite complexity of nature. The concept has been used to measure coastlines, clouds and other natural phenomena and had far-reaching effects in physics, biology and astronomy.
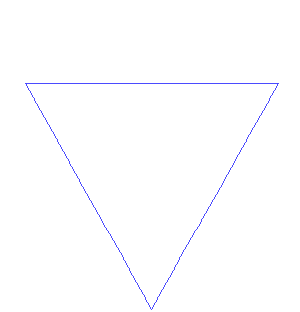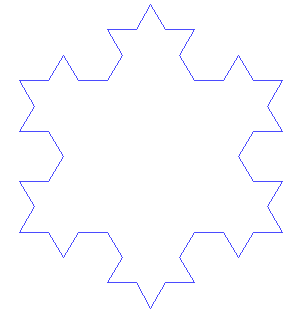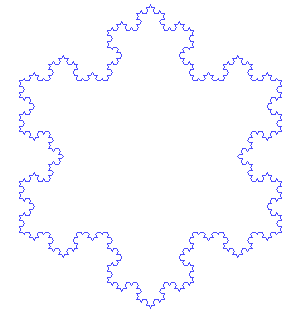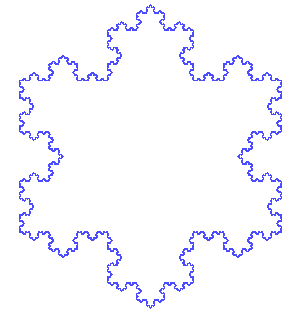
To create a Koch snowflake, one begins with an equilateral triangle and then replaces the middle third of every line segment with a pair of line segments that form an equilateral "bump." One then performs the same replacement on every line segment of the resulting shape, ad infinitum. With every iteration, the perimeter of this shape increases by one third of the previous length. The Koch snowflake is the result of an infinite number of these iterations, and has an infinite length, while its area remains finite. For this reason, the Koch snowflake and similar constructions were sometimes called "monster curves."
Additional examples of fractals include the Lyapunov fractal and the limit sets of Kleinian groups. Fractals can be deterministic (all the above) or stochastic (that is, non-deterministic). For example, the trajectories of the Brownian motion in the plane have a Hausdorff dimension of 2.
Chaotic dynamical systems are sometimes associated with fractals. Objects in the phase space of a dynamical system can be fractals. Objects in the parameter space for a family of systems may be fractal as well. An interesting example is the Mandelbrot set.

Julia Set

Cantor Set


Sierpinski Triangle

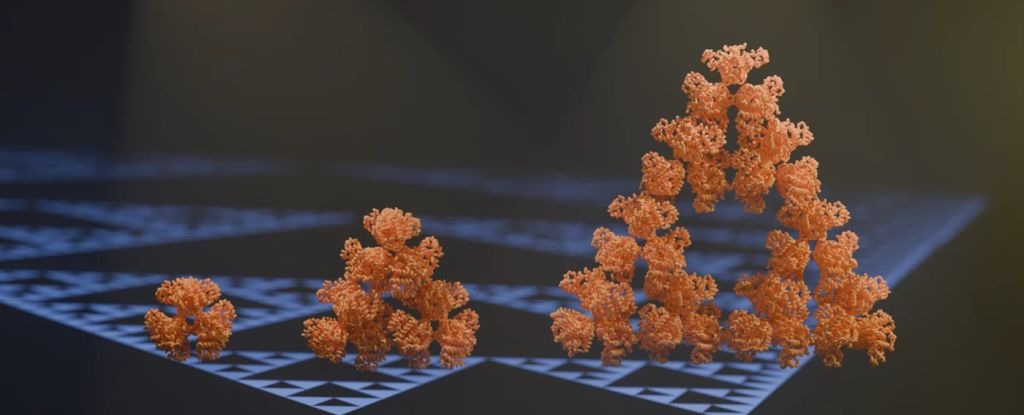
First Fractal Molecule in Nature Assembles Into a Sierpinski Triangle And We Don't Know Why
Science Alert - April 16, 2024