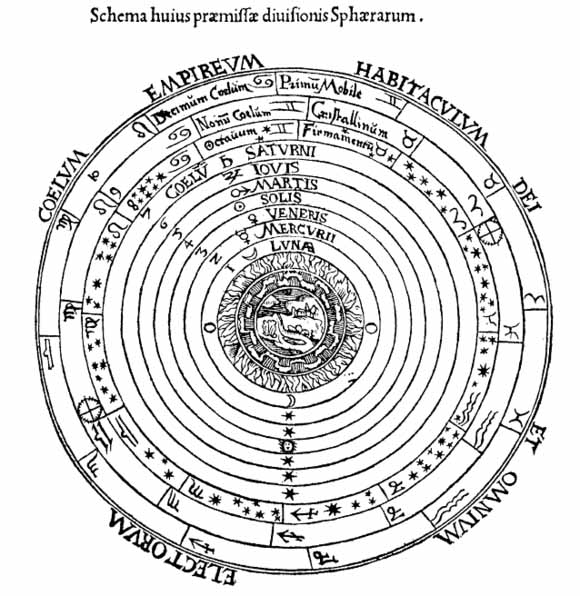

The celestial spheres, or celestial orbs, were the fundamental celestial entities of the cosmological celestial mechanics first invented by Eudoxus, adopted by Aristotle and developed by Ptolemy, Copernicus and others. In this celestial model the stars and planets are carried around by being embedded in rotating spheres made of an aetherial transparent fifth element (quintessence), like jewels set in orbs.
In geocentric models the spheres were most commonly arranged outwards from the center in this order: the sphere of the Moon, the sphere of Mercury, the sphere of Venus, the sphere of the Sun, the sphere of Mars, the sphere of Jupiter, the sphere of Saturn, the starry firmament, and sometimes one or two additional spheres. The order of the lower planets was not universally agreed: Plato and his followers ordered them Moon, Sun, Mercury, Venus, and then followed the standard model for the upper spheres; there were other disagreements about the relative place of the spheres of Mercury and Venus. The Celestial Sphere
In his Metaphysics, Aristotle adopted a celestial physics of geo-concentric rotating nested spheres first devised and developed by the astronomers Eudoxus and Callippus. In the fully developed Aristotelian celestial physics, the spherical Earth is at the center of the universe and the planets are attached to anywhere from 47 to 55 concentric spheres that rotate around the Earth. Aristotle considers that these spheres are made of an unchanging fifth element, the aether, and each of these concentric spheres is moved by a god - an unchanging divine mover. Aristotle says that to determine the exact number of spheres and the number of divine movers, one should consult the astronomers.
The astronomer Ptolemy (fl. ca. 150 AD) defined a geometrical model of the universe in his Almagest and extended it to a physical model of the cosmos in his Planetary hypotheses. In doing so, he added mathematical detail and predictive accuracy that had been lacking in earlier spherical models of the cosmos. In Ptolemy's model, each planet is moved by two or more spheres (or strictly speaking, by thick equatorial slices of spheres): one sphere is the deferent, with a center offset somewhat from the Earth; the other sphere is an epicycle embedded in the deferent, with the planet embedded in the spherical epicycle. Through the use of the epicycle, eccentric, and equant, this model of compound circular motions could account for all the irregularities of a planet's apparent movements in the sky.
Christian and Muslim philosophers modified Ptolemy's system to include an unmoved outermost region, which was the dwelling place of God and all the elect. The outermost moving sphere, which moved with the daily motion affecting all subordinate spheres, was moved by a fixed unmoved mover, the Prime Mover, who was identified with God. Each of the lower spheres was moved by a subordinate spiritual mover (a replacement for Aristotle's multiple divine movers), called an intelligence.
Around the turn of the millennium, the Arabian astronomer and polymath Ibn al-Haytham (Alhacen) presented a development of Ptolemy's geocentric epicyclic models in terms of nested spheres. Despite the similarity of this concept to that of Ptolemy's Planetary Hypotheses, al-Haytham's presentation differs in sufficient detail that it has been argued that it reflects an independent development of the concept. In chapters 15-16 of his Book of Optics, Ibn al-Haytham also discovered that the celestial spheres do not consist of solid matter.
Near the end of the twelfth century, the Spanish-Arabian Muslim astronomer al-Bitruji (Alpetragius) sought to explain the complex motions of the planets using purely concentric spheres, which moved with differing speeds from east to west. This model was an attempt to restore the concentric spheres of Aristotle without Ptolemy's epicycles and eccentrics, but it was much less accurate as a predictive astronomical model.
In the thirteenth century, scholars in European universities dealt with the implications of the rediscovered philosophy of Aristotle and astronomy of Ptolemy. One issue that arose concerned the nature of the celestial spheres. Through an extensive examination of a wide range of scholastic texts, Edward Grant has demonstrated that scholastic philosophers generally considered the celestial spheres to be solid in the sense of three-dimensional or continuous, but most did not consider them solid in the sense of hard. The consensus was that the celestial spheres were made of some kind of continuous fluid.
Early in the sixteenth century Nicolaus Copernicus drastically reformed the model of astronomy by displacing the Earth from its central place in favour of the sun, yet he called his great work De revolutionibus orbium coelestium (On the Revolutions of the Celestial Spheres). Although Copernicus does not treat the physical nature of the spheres in detail, his few allusions make it clear that, like many of his predecessors, he accepted non-solid celestial spheres.
However, it seems a crucial physical reason for his heliocentrism in order to save the celestial spheres may have been that he rejected the possibility of interpenetrating spheres, but for some reason thought Martian parallax at opposition is greater than solar parallax, whereby Mars must then be nearer the Earth than the sun is, but also whereby the Martian and solar spheres must intersect on all geocentric and geoheliocentric planetary models. They can only be non-intersecting with Mars less than 1 AU away at opposition in the pure heliocentric model. As Copernicus's pupil and herald Rheticus expressed this in his 1540 Copernican Narratio Prima published 3 years before Copernicus's De Revolutionibus, "Mars unquestionably shows a parallax sometimes greater than the sun's, and therefore it seems impossible that the earth should occupy the centre of the universe.". But this is only an impossibility for a spherist cosmology in which different planetary spheres cannot intersect, but not for non-spherist astronomy, as illustrated by the non-spherist Tychonic geocentric model, for example, in which the Martian and solar orbits intersect (as also do the orbits of Mercury and Venus with those of Mars and of Jupiter as drawn).
Tycho Brahe's observations that the comet of 1577 displayed less daily parallax than the Moon implied it was superlunary and so, impossibly, must pass through some planetary orbs in its transit. This led him to conclude that "the structure of the heavens was very fluid and simple." Tycho opposed his view to that of "very many modern philosophers" who divided the heavens into "various orbs made of hard and impervious matter." Since Grant has been unable to identify such a large number of believers in hard celestial spheres before Copernicus, he concludes that the idea first became dominant sometime after the publication of Copernicus's De revolutionibus in 1542 and either before, or possibly somewhat after, Tycho Brahe's publication of his cometary observations in 1588.
In Johannes Kepler's celestial physics the spheres were regarded as the purely geometrical spatial regions containing each planetary orbit rather than physical bodies as rotating orbs as in preceding Aristotelian celestial physics. The eccentricity of each planet's elliptical orbit and its major and minor axes thereby defined the lengths of the radii of the inner and outer limits of its celestial sphere and thus its thickness. The intermediate causal role of these annular geometrical spheres in Kepler's Platonist geometrical cosmology is to determine the sizes and orderings of the five Platonic polyhedra within which the spheres were supposedly spatially embedded.
Thus in Kepler's celestial mechanics the previous ultimate causal role of the spheres became a non-ultimate intermediate role as the ultimate causal focus shifted on the one hand to the Platonic regular polyhedra within which Kepler held they were embedded and which thus ultimately defined the dimensions and eccentricities of planetary orbits, and on the other hand to the rotating sun as the central inner driver of planetary motion, itself rotated by its own motor soul. However, an immobile stellar sphere was a lasting remnant of physical celestial spheres in Kepler's cosmology.
But solid physical spheres still featured in both Galileo's and Newton's early celestial mechanics, with Galileo initially considering the planets to be rolling around the upper surfaces of fixed perfectly smooth spheres driven by their own impetus and gravity, and with Newton calculating the centrifugal pressure that would be exerted by the Moon on the lower concave surface of the lunar orb in his 1660s analysis of lunar gravity. Thus for a long time Galileo fiercely resisted the Tychonic theory that comets are superlunary because it destroyed his initial spherist celestial mechanics by knocking away the counter-gravitational supporting surfaces of the rolling planets, and he was unable to explain circular orbits as closed curve projectiles driven by a centrifugal impetus and centripetal gravity.
In Cicero's Dream of Scipio, the elder Scipio Africanus describes an ascent through the celestial spheres, compared to which the Earth and the Roman Empire dwindle into insignificance. A commentary on the Dream of Scipio by the late Roman writer Macrobius, which included a discussion of the various schools of thought on the order of the spheres, did much to spread the idea of the celestial spheres through the Early Middle Ages.

Some late medieval figures inverted the model of the celestial spheres to place God at the center and the Earth at the periphery. Near the beginning of the fourteenth century Dante, in the Paradiso of his Divine Comedy, described God as a light at the center of the cosmos. Here the poet ascends beyond physical existence to the Empyrean Heaven, where he comes face to face with God himself and is granted understanding of both divine and human nature.